Ускорение бруска при угле наклона доски к горизонту

Обновлено: 13.05.2024

[latexpage]Под движением по наклонной плоскости понимают перемещение тела вдоль плоской поверхности, которая расположена под определенным углом к горизонту. Для расчета характеристик данного движения нужно установить, какие силы, действуют на движущееся тело (или покоящее). Чаще всего при решении задач на движение тела при наклонной плоскости сила трения неизвестна. Поэтому приходится определять ее из соответствующей системы уравнений движения. При решении задач на наклонную плоскость наиболее удобно использовать систему координат, которую мы укажем ниже. Использование такой системы координат позволяет минимизировать количество тригонометрических функций угла (синусов и косинусов) при нахождении проекций векторов.

Пример. На какую высоту надо поднять край доски длиной 2 м, чтобы по ней можно было равномерно поднимать груз массой 100 кг, прикладывая к нему силу 160 Н, направленную вдоль доски? Коэффициент трения равен 0,4.

Решение. 1. Систему отсчета свяжем с доской, относительно которой движется тело, поскольку, очевидно, что она будет неподвижна относительно Земли в тот момент времени, когда груз будет двигаться по ней, а значит эта система является инерциальной. Координатную ось $Ox$ направим вдоль наклонной плоскости в направлении движения тела. Координатную ось $Oy$ направим так, чтобы она проходила перпендикулярно наклонной плоскости в направлении вектора силы реакции опоры $\overrightarrow$.

2. Выполним чертеж с указанием всех сил, действующих на тело.

3. Запишем второй закон Ньютона, учитывая, что в тот момент, когда груз начнет двигаться, его ускорение будет равно нулю

Проекции на координатные оси:

$Oy: N- mg cos \alpha = 0 $.

$mg sin \alpha — \mu mg cos \alpha =0$.

5. Кинематические уравнения в данной задаче не требуются, поэтому переходим к п.6.

6. Из последнего уравнения найдем тангенс угла наклона доски

$mg sin \alpha — \mu mg cos \alpha =0 \Rightarrow sin \alpha — \mu cos \alpha =0$,
$tg \alpha = \mu$.

Высоту, на которую нужно поднять доску можно найти из условия ($L$ — длина доски, гипотенуза прямоугольного треугольника)

$\frac=sin\alpha \Rightarrow h=L sin\alpha $.

Известно, что $tg^2\alpha +1=\frac$, выведем отсюда формулу для нахождения синуса

Пример. Брусок массой 10 кг находится на наклонной плоскости с углом наклона 30°. Коэффициент трения между бруском и плоскостью равен 0,6. Какую направленную вдоль наклонной плоскости силу надо приложить к бруску, чтобы сдвинуть его вдоль наклонной плоскости вверх?

Решение. 1. Систему отсчета свяжем с доской, относительно которой движется тело, поскольку, очевидно, что она будет неподвижна относительно Земли, а значит эта система является инерциальной. Координатную ось $Ox$ направим вдоль наклонной плоскости в направлении движения тела. Координатную ось $Oy$ направим так, чтобы она проходила перпендикулярно наклонной плоскости в направлении вектора силы реакции опоры $\overrightarrow$.

2. Выполним чертеж с указанием всех сил, действующих на тело.

3. Запишем второй закон Ньютона, учитывая, что тело движется равномерно:

Проекции на координатные оси:

$Oy: N- mg cos \alpha = 0 $.

$F-mg sin \alpha — \mu mg cos \alpha =0$.

5. Кинематические уравнения в данной задаче не требуются, поэтому переходим к п.6.

6. Из последнего уравнения найдем $F=mg sin \alpha + \mu mg cos \alpha =mg (sin \alpha + \mu cos \alpha)$, т.е.

$F=10\cdot 10\cdot \left ( sin\, 30^+0,6\cdot cos\, 30^ \right ) \approx 102$ Н.

Пример. При каком коэффициенте трения μ брусок скользит по наклонной плоскости с углом наклона α = 30° с ускорением 3,5 м/с?

Решение. 1. Систему отсчета свяжем с наклонной плоскостью, относительно которой движется тело, поскольку, очевидно, что она будет неподвижна относительно Земли, а значит эта система отсчета является инерциальной. Координатную ось $Ox$ направим вдоль наклонной плоскости в направлении движения тела. Координатную ось $Oy$ направим так, чтобы она проходила перпендикулярно наклонной плоскости в направлении вектора силы реакции опоры $\overrightarrow$.

2. Выполним чертеж с указанием всех сил, действующих на тело.

Проекции на координатные оси:

$Oy: N- mg cos \alpha = 0 $.

$mg sin \alpha — \mu mg cos \alpha =ma$.

5. Кинематические уравнения в данной задаче не требуются, поэтому переходим к п.6.

6. В последнем уравнении, после сокращения массы, получим

$g sin \alpha — \mu g cos \alpha =a$,

$g sin \alpha — a =\mu g cos \alpha$,

Пример. Санки равномерно скатываются с горы, угол наклона которой к горизонту α = 30°. Каков должен быть наименьший угол β, образуемый веревкой с поверхностью горы, чтобы санки тянуть равномерно в гору?

Решение. Рассмотрим первое условие задачи: «Санки равномерно скатываются с горы, угол наклона которой к горизонту α = 30°». Используем это условие, чтобы найти коэффициент трения санок о горку.

1. Систему отсчета свяжем с горкой, так как эта система отсчета является инерциальной. Координатную ось $Ox$ направим вдоль наклонной плоскости в направлении движения тела. Координатную ось $Oy$ направим так, чтобы она проходила перпендикулярно наклонной плоскости в направлении вектора силы реакции опоры $\overrightarrow$.

2. Выполним чертеж с указанием всех сил, действующих на тело.

3. Запишем второй закон Ньютона, учитывая, что санки скатываются равномерно

Проекции на координатные оси:

$Oy: N- mg cos \alpha = 0 $.

$mg sin \alpha — \mu mg cos \alpha =0$.

5. Кинематические уравнения в данной задаче не требуются, поэтому переходим к п.6.

6. В последнем уравнении, после сокращения массы, получим

$g sin \alpha — \mu g cos \alpha =0$,

$g sin \alpha =\mu g cos \alpha$,

Рассмотрим второе условие задачи и найдем условие при котором под действие силы, приложенной под углом β к наклонной плоскости, санки можно будет тянуть равномерно вверх.

1. Систему отсчета по-прежнему свяжем с горкой. Координатную ось $Ox$ направим вдоль наклонной плоскости. Координатную ось $Oy$ направим так, чтобы она проходила перпендикулярно наклонной плоскости в направлении вектора силы реакции опоры $\overrightarrow$.

2. Выполним чертеж с указанием всех сил, действующих на тело.

3. Запишем второй закон Ньютона, учитывая, что тело движется равномерно:

Проекции на координатные оси:

$Oy: N- mg cos \alpha +Fsin\, \beta= 0 $.

$Fcos\, \beta-mg sin \alpha — \mu (mg cos \alpha-Fsin\, \beta) =0$.

5. Кинематические уравнения в данной задаче не требуются, поэтому переходим к п.6.

6. Из последнего уравнения найдем

Из последнего уравнения видно, что значение силы будет определено при любом значении угла $0\leqslant \beta \leq \frac<\pi >$. Минимальным же углом, будет являться угол $\beta =0$.

Задачи для самостоятельного решения.

1. На плоскости, угол наклона которой к горизонту можно изменять, находится шайба. При некотором угле наклона $$ шайба соскальзывает с плоскости с ускорением a = g/2. С каким ускорением будет соскальзывать эта шайба, если угол наклона плоскости будет $-\alpha >$? Коэффициент трения шайбы о поверхность плоскости μ = 0,5.

$a= g( cos\alpha — \mu sin \alpha ) = 1,96$ м/с 2 .

2. Санки можно удержать на ледяной горке с углом наклона α = 12° силой, не меньшей F = 50 Н. Чтобы тянуть сани в гору равномерно, силу тяги нужно увеличить на ∆F = 10 Н. С каким ускорением с этой горки будут двигаться санки, если их предоставить самим себе?

3. С каким ускорением соскальзывают санки массой m = 10 кг с горки с углом наклона α = 30° к горизонту, если их тянут вниз с постоянной горизонтальной силой F = 50 Н? Коэффициент трения санок о поверхность горки μ = 0,2.

4. Какую силу необходимо приложить к нити, составляющей угол β = 30° с наклонной плоскостью, чтобы за эту нить равномерно тащить брусок массой m = 0,5 кг? Коэффициент
трения между бруском и плоскостью μ = 0,4. Угол между плоскостью и горизонтом α = 45°

5. Деревянный брусок массой m = 0,5 кг положили на наклонную плоскость. С какой наименьшей силой, направленной перпендикулярно поверхности плоскости, нужно прижать брусок, чтобы он лежал на грани соскальзывания? Коэффициент трения бруска о плоскость μ = 0,4. Угол наклона плоскости к горизонту α = 30°

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Многие школьники, поступающие в вузы, часто испытывают затруднения при решении задач, в которых действуют силы трения.

Вспомним об основных особенностях сил так называемого сухого трения — трения между двумя твердыми телами. Эти силы возникают всегда при непосредственном соприкосновении тел, направлены вдоль поверхности соприкосновения и действуют на каждое из соприкасающихся тел, причем действуют так, чтобы препятствовать движению одного тела относительно другого — если это силы трения скольжения, или так, чтобы препятствовать самому возникновению этого движения — если речь идет о силах трения покоя.

Абсолютная величина силы трения скольжения F_тp зависит от вида трущихся поверхностей и силы N нормального давления одного тела на другое:

где μ— коэффициент трения.

Сила трения покоя F_{тp п} всегда уравновешивает все остальные силы, действующие на тело вдоль поверхности соприкосновения. Ее абсолютная величина может принимать любые значения от нуля до некоторого максимального значения F_{тp п} _max , которое обычно считают равным F_тp_ск:

При решении задач прежде всего необходимо разобраться, с какими именно силами трения — покоя или скольжения — мы имеем дело. Рассмотрим несколько конкретных задач.

Задача 1. Ни горизонтальном столе лежат два бруска массой Μ₁ =7 кг и М₂ = 10 кг, связанные нитью. Еще одна нить, привязанная к бруску массой Μ₁, переброшена через блок, укрепленный на краю стола, и к ней подвешен груз массой m = 1 кг (рис. 1). Коэффициент трения между брусками и столом μ = 0,1. Определите натяжения обеих нитей и силы трения, действующие на каждый из брусков.

Во-первых, выясним, будут двигаться бруски или нет. Они могут начать двигаться под действием силы натяжения Т₁ правой нити, а она, по абсолютной величине, не может превысить силу тяжести груза массой m:

Максимальное значение силы трения покоя для обоих брусков

Так как Т₁ < F_{тp п} _max , бруски покоятся. Очевидно, что покоится и груз массой m; следовательно,

Теперь рассмотрим но отдельности бруски массой M ₁ и М₂. На правый брусок действуют силы натяжения нитей T ₁ и T ₂ и сила трения F_тp₁ (рис. 2) (нас интересуют только те силы, которые лают горизонтальные проекции, отличные от нуля).

Максимальное значение силы трения

значит, одна только сила трения не может уравновесить брусок. Как только она достигнет своего наибольшего значения, натянется вторая нить — появится сила натяжения Т₂.

Первый брусок будет покоиться, если

На второй брусок действуют две силы: сила натяжения нити Т₂ и сила трения F_тр2 (рис. 3). Поскольку

сила трения F_тp2 может уравновесить силу Т₂:

Задача 2. Брусок лежит на доске. Доску приподнимают за один край. Как зависит абсолютная величина силы трения, действующей на брусок, от угла наклона доски α (рис. 4)? Коэффициент трения между бруском и доской μ, масса бруска m.

При достаточно малых углах наклона брусок покоится на доске. При этом сила трения покоя F_{тр п} уравновешивает силу F — составляющую силы тяжести бруска, направленную вдоль наклонной плоскости:

С увеличением угла α сила трения покоя растет, и при некотором угле α₀ она достигает своего максимального значения:

При дальнейшем увеличении угла α тело скользит по доске, и сила трения является силой трения скольжения:

График зависимости абсолютной величины силы трения от утла наклона доски α показан на рисунке 5: до угла α₀ сила трения возрастает по закону синуса, а дальше она убывает по закону косинуса.

Задача 3. Прямоугольный брусок, размеры которого показаны на рисунке 6, тянут равномерно по горизонтальной плоскости за веревку, угол наклона которой α можно менять. Коэффициент трения бруска о плоскость равен μ. При какой величине угла α₀ брусок начнет приподниматься?

Рассмотрим все силы, которые действуют на брусок. Это сила натяжения веревки Т, сила тяжести m∙g, сила реакции опоры N (равная по абсолютной величине силе нормального давления) и сила трения скольжения F_{тр ск} (так как брусок движется). При угле наклона α₀, когда брусок начнет приподниматься, силы N и F_{тр ск} проходят через точку А (рис. 7).

Так как брусок движется равномерно и прямолинейно, сумма действующих на него сил и сумма моментов этих сил относительно любой оси должны быть равны нулю. Следовательно, равны нулю сумма проекций всех сил на ось X:

и сумма моментов сил относительно центра тяжести С:

Из этих двух уравнении с учетом того, что F _{тр ск} = μ∙ N , получаем

Задача 4. Ребенок скатывается с горки на санках. Высота горки Η = 15 м, угол наклона к горизонту α = 30º, а коэффициент трения линейно нарастает вдоль пути от μ₁ = 0 у вершины горы до μ₂ = 0,4 у подножия. Какую скорость будут иметь санки у подножия горы?

Так как абсолютная величина силы трения скольжения при движении санок изменяется, а значит, движение санок не будет равноускоренным, задачу проще и удобнее решать с помощью закона сохранения энергии:

Здесь m·g·H — потенциальная энергия санок на вершине горы, — их кинетическая энергия у подножия и A — работа против силы трения скольжения F_{тp ск.}.

Для определения A нарисуем график зависимости F_{тp ск.} от пути s (рис. 8). У вершины горы

Работа А численно равна площади заштрихованного треугольника на рисунке 8:

Тогда из закона сохранения энергии получаем:

1. Брусок массой m, размеры которого показаны на рисунке 9, стоит на наклонной плоскости с углом наклона α. На брусок начинает действовать сила F , параллельная наклонной плоскости. При каком абсолютном значении этой силы брусок опрокинется? Известно, что соскальзывать с наклонной плоскости брусок при этом не будет.

2. Какую работу нужно затратить, чтобы втащить сани с грузом (общей массой m = 30 кг) на горку высотой H = 10 м? Угол наклона горки к горизонту α = 30°, а коэффициент трения между санями и горкой линейно убывает вдоль пути от μ₁ = 0,5 у подножия до μ₂ = 0,1 у вершины.

3. Мешок с мукой сползает без начальной скорости с высоты Н = 2 м по доске, наклоненной под углом α₂ = 45° к горизонту. После спуска мешок попадает на горизонтальную поверхность. Коэффициент трения мешка о доску и горизонтальную поверхность μ = 0,5. На каком расстоянии от конца доски мешок остановится?

Брусок сползает без начальной скорости с высоты 2 м по доске, наклоненной под углом 45° к горизонту. После спуска брусок попадает на горизонтальный пол. Коэффициенты трения бруска о доску и пол одинаковы и равны 0,5. На каком расстоянии от конца доски остановится брусок?

Задача №2.3.12 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Решение задачи:

Проще всего эту задачу можно решить, используя закон сохранения энергии, по которому работа неконсервативной силы (силы трения в данном случае) равна изменению полной механической энергии бруска.

Когда брусок остановится, пройдя путь $S$ по полу, его полная механическая энергия станет равной нулю, хотя в начале она была равна $mgH$ (потенциальная энергия). Поэтому изменение энергии $\Delta E$ равно:

\[\Delta E = 0 – mgH = – mgH\;\;\;\;(2)\]

Так как сила трения принимает разные значения на разных участках движения, то работу найдем как следующую сумму:

Рассмотрим 1-й участок: участок движения по доске. Брусок покоится вдоль оси $y$, поэтому согласно первому закону Ньютона верно записать следующее:

\[N_1 = mg \cdot \cos \alpha \]

Сила трения скольжения определяется по следующей известной формуле:

Эта сила совершит отрицательную работу, равную по определению:

\[ = – \mu mg \cdot \cos \alpha \cdot l\]

Обратите внимание, что произведение $\left( \right)$ равно $L$ (смотрите схему). Но поскольку мы не знаем значения $L$, выразим её через угол $\alpha$ и высоту $H$.

\[L = l \cdot \cos \alpha = H \cdot ctg\alpha \]

Тогда работа $A_1$ равна:

Теперь перейдём ко 2-ому участку: участку движения по полу. Аналогично определим силу реакции опоры:

Сила трения скольжения станет больше за счёт увеличения $N$, её можно определить по той же общей формуле:

На втором участке сила трения совершит работу $A_2$, определяемую формулой:

Соберем выражения (2), (3), (4) и (5) в (1), получим:

\[ – \mu mgH \cdot ctg\alpha – \mu mgS = – mgH\]

Сократим на $mg$ и домножим на $-1$, тогда:

\[\mu H \cdot ctg\alpha + \mu S = H\]

В итоге получим такое решение задачи в общем виде:

\[S = H\left( <\mu >– ctg\alpha > \right)\]

\[S = 2\left( > – ctg45^\circ > \right) = 2\; м\]

Ответ: 2 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

Добрый день. А можно ли в данной задаче, понимая, что треугольник со сторонами Н и L равнобедренный, т.к. углы у основания 45 градусов, следовательно L будет равно Н и не нужно заморачиваться с котангенсом

Разумеется можно

Здравствуйте, а можно эту задачу решить через скорость и ускорение?То есть через скорость в момент когда брусок переходит на горизонтальную поверхность? Если да, то можете написать как, буду очень признателен.

Да, можно. Не буду максимально всё расписывать, иначе тут выйдет очень много текста.
Запишем второй закон Ньютона в проекции на ось $x$ для бруска, движущегося по наклоненной доске:
\[m = mg\sin \alpha – \mu mg\cos \alpha \]
Откуда ускорение бруска при движении по наклоненной доске равно:
\[ = g\left( \right)\]
Аналогично запишем второй закон Ньютона в проекции на ось $x$ для бруска, движущегося по полу:
\[m = \mu mg\]
Откуда ускорение бруска при движении по полу равно:
\[ = \mu g\]
Воспользуемся дважды формулой кинематики без времени:
\[\left\< \begin
<\upsilon ^2>= 2l \hfill \\
<\upsilon ^2>= 2S \hfill \\
\end \right.\]
Откуда имеем:
\[l = S\]
\[S = \frac<<>><<>>l\]
\[S = \frac <><<\mu g>>l\]
\[S = \left( <\mu >\sin \alpha – \cos \alpha > \right)l\]
Из прямоугольного треугольника видно, что:
\[l = \frac>\]
Тогда:
\[S = H\left( <\mu >– ctg\alpha > \right)\]
Как Вы видите, мы получили абсолютно такой же ответ.

Задания Д14 B25 № 4096

Брусок лежит на горизонтальной деревянной доске. Доску начали медленно наклонять и заметили, что брусок начал соскальзывать с неё в момент, когда доска составляла с горизонтом угол 30°. Точность измерения угла составляет ±2°. Этот опыт свидетельствует о том, что коэффициент трения бруска о доску

2) лежит в диапазоне от до

3) лежит в диапазоне от до

4) лежит в диапазоне от до

Определим, как связан коэффициент трения с углом наклона доски при котором брусок начинает соскальзывать. Для этого рассмотрим все силы, действующие на брусок, и выпишем второй закон Ньютона. Так как нас интересует пограничная ситуации (брусок вот-вот готов начать соскальзывать вниз), ускорение бруска нужно положить равным нулю.

В проекциях на оси параллельную и перпендикулярную доске получаем: Откуда для коэффициента трения имеем:

Поскольку точность измерения угла составляет ±2° и было зафиксировано, что брусок начал соскальзывать с доски в момент, когда она составляла с горизонтом угол 30°, заключаем, что минимальное и максимальное значения угла, при котором это произошло равны: Отсюда сразу получаем, что коэффициент трения бруска о доску лежит в диапазоне от до

Примечание: Ответ на данную задачу можно получить, оценив погрешность измерения коэффициента трения по погрешности измерения угла. Для этого может пригодиться следующая формула для погрешности величины, определяемой косвенным образом.

Постановка задачи следующая. Пусть известна зависимость некоторой величины y от других величин (например, ), и пусть последние мы можем определить на эксперименте (естественно, с некоторой погрешностью). Тогда по известной зависимости можно определить величину При этом возникает вопрос о погрешности с которой мы получили данное значение, а именно: как эта погрешность связана с погрешностями величин Решение дает следующая формула:

В данном случае, есть всего одна переменная Величину естественное, необходимо измерять в радианах. Имеем:

Откуда сразу получается оценка для для диапазона изменения коэффициента трения:

Динамика и кинематика - это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.

Основная формула динамики

Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:

Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.

В случае движения вращения второй закон Ньютона записывается в виде:

Здесь M и I - моменты силы и инерции, соответственно, α - угловое ускорение.

Формулы кинематики

Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:

Здесь v₀ - значение начальной скорости тела, S - пройденный за время t путь вдоль прямолинейной траектории. Знак "+" следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак "-". Это важный момент.

Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:

Здесь α и ω - угловые ускорение и скорость, соответственно, θ - угол поворота вращающегося тела за время t.

Линейные и угловые характеристики друг с другом связаны формулами:

Здесь r - радиус вращения.

Движение по наклонной плоскости: силы

Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.

Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:

тяжести;
реакции опоры; и/или скольжения;
натяжение нити;
сила внешней тяги.

Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.

Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.

Методика решения

Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.

Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:

Где N - реакция опоры, µ - коэффициент трения, не имеющий размерности.

Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:

Здесь φ - это угол наклона плоскости к горизонту.

Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.

В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:

Где F_r - сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, F_r создает следующий момент:

Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.

Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.

Задача на движение бруска по наклонной плоскости

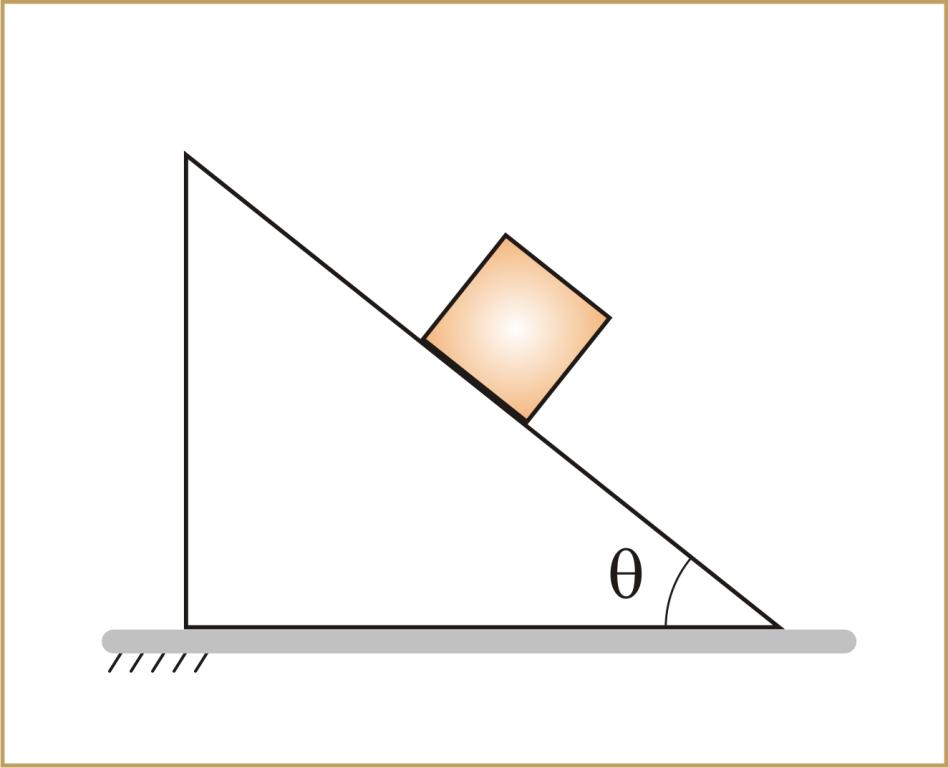
Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45 o . Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.

Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:

Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:

Откуда следует выразить время, и подставить известные значения:

Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.

Задача со скатывающимся по плоскости цилиндром

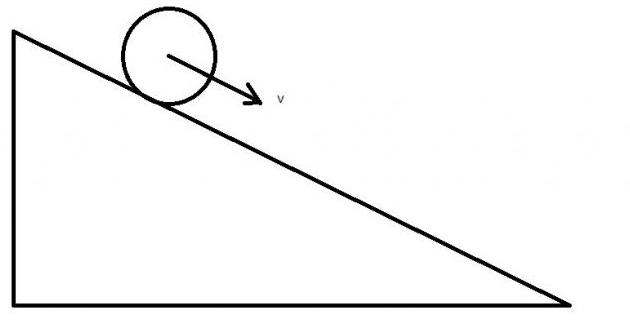
Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30 o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.

Запишем соответствующие уравнения:

Момент инерции I цилиндра вычисляется по формуле:

Подставим это значение во вторую формулу, выразим из нее силу трения F_r и заменим полученным выражением ее в первом уравнении, имеем:

Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.

Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:

Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:

Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.

Читайте также: