Как называется тангенс угла наклона касательной проведенной к диаграмме бетона из начала координат

Обновлено: 30.04.2024

В химической технологии чрезвычайно важное значение имеют процессы массопередачи. Их сущность состоит в переходе вещества из одной фазы в другую в направлении достижения равновесия. В промышленности широко распространены следующие процессы массопередачи: абсорбция, перегонка, ректификация, адсорбция, сушка, экстракция и кристаллизация. Во многих случаях массообменные процессы сопровождаются выделением или поглощением теплоты, что оказывает влияние на их скорость.

Для определения направления и скорости массообменного процесса необходимо знать состав веществ. Пусть смесь состоит из двух компонентов — А и В. Для этой системы способы выражения состава фаз представлены в табл. 17.1.

Равновесие между фазами.Перенос массы из одной фазы в другую происходит до тех пор, пока не будет достигнуто равновесие между фазами — термодинамическое состояние системы, при котором скорости прямого и обратного процессов равны.

В общем виде связь между составом фаз при равновесии может быть выражена зависимостью Таблица 17.1

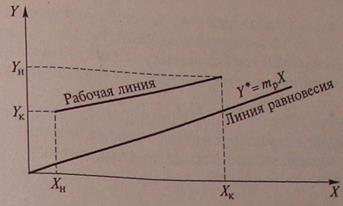
Рис. 17.1. Линия равновесия и рабочая линия массообменного аппарата:

— начальная и конечная относительные мольные доли целевого компонента в газовой фазе; — начальная и конечная относительные мольные доли этого компонента в жидкой фазе; — его равновесная относительная мольная доля в газовой фазе; — коэффициент распределения

где — равновесная относительная мольная доля целевого компонента в газовой (паровой) фазе. Графическое изображение этой зависимости называется линией равновесия (рис. 17.1).

Отношение составов фаз при равновесии

называется коэффициентом распределения.

Коэффициент распределения — это тангенс угла наклона линии равновесия. Если она имеет форму кривой, то является тангенсом угла наклона касательной к данной точке этой линии.

до Y_K (на выходе из аппарата). Соответственно относительная мольная доля этого же компонента в жидкой фазе увеличивается (на входе в аппарат) до (на выходе из аппарата). Тогда мольный расход компонента, перешедшего из газовой фазы,

где — мольный расход газовой фазы, а мольный расход

компонента, перешедшего в жидкую фазу,

где — мольный расход жидкой фазы.

Поскольку речь идет о переходе одного и того же компонента справедливо приравнять правые части уравнений (17.1) и (17.2):

Для произвольного сечения аппарата, в котором текущие составы целевого компонента равны Y и X, уравнение материального баланса для верхней части аппарата имеет вид:

Выражение (17.3) называется уравнением линии рабочих концентраций (рабочей линией) и представляет собой уравнение прямой линии с тангенсом угла наклона . Рабочая линия для всего аппарата ограничена точками с координатами и (см. рис. 17.1).

Деформативные свойства бетона определяются его начальным модулем упругости Е_b. Этот модуль может быть определен в зависимости от марки или класса бетона по таблице ниже.

Начальные модули упругости тяжелого бетона

Модуль упругости Е_b·10 -3 МПа

За начальный модуль упругости бетона при сжатии и растяжении принимается отношение нормального напряжения в бетоне к его относительной деформации при величине напряжения σ_b < 0,2R_b. Упругие свойства бетона следует проверить путем эксперимента, определив начальный модуль упругости в_ь = 0,2R_b и условный модуль деформаций при σ_b = 0,2R_b, подвергнув осевому сжатию призму размером 100x100x300 мм, замеряя деформацию ε = Δl/l.

При однократном непрерывном сжатии бетонного образца максимальной разрушающей нагрузкой диаграмма напряжения-деформации имеет криволинейное очертание, деформации в бетоне растут быстрее напряжений (рис. ниже). Такой характер диаграммы возникает, потому что при быстром достижении максимального усилия в бетоне под действием нагрузки одновременно с упругими деформациями развиваются также неупругие, обусловленные ползучестью бетона. Ползучесть — это способность бетона деформироваться во времени даже при неизменной нагрузке.

Диаграммы напряжения-деформации бетона при сжатии

В момент окончательного разрушения призмы получают расчетное сопротивление R_b. После этого строится график с откладыванием по оси х относительного удлинения, а по оси у — напряжения в бетоне (рис. выше).

1. начальный модуль упругости при напряжении σ_b = 0,2R_b (тангенс угла наклона касательной к действительной диаграмме σ-ε в начале координат)

2. с увеличением напряжений угол наклона касательной к кривой σ_b-ε_b будет уменьшаться (вследствие развития во времени деформаций ползучести). Находят тангенс угла наклона к оси абсцисс касательной, проведенной к этой кривой,

3. определяют условный модуль упругости (средний модуль упругопластичности бетона) при σ_b = 0,5R_b (тангенс угла наклона секущей к кривой полных деформаций)

4. выражая модуль упргопластичности бетона через модуль упругости (из выражений выше), получают коэффициент упругости бетона (коэффициент Пуассона)

Коэффициент Пуассона (отношение поперечной деформации к продольной) с увеличением напряжений в бетоне возрастает: начальное его значение принимается равным 0,2.

Призменная прочность бетона может быть получена по формуле

где N_max — разрушающая нагрузка, кН; А — площадь сечения образца, см 2 .

Значит, верна формула: \(f'(x_0)=\mathrm\, \alpha=k\) .

Заметим, что координаты точки \(A\) тогда можно записать как \( \ (x_0; f(x_0)) \ \) или \( \ (x_0; y_0) \ \) ,
где \( \ y_0=kx_0+b\) .
То есть \( \ y_0=f(x_0)\) .

На рисунке изображены график функции \(y = f(x)\) и касательная к нему в точке с абсциссой \(x_0\) . Найдите значение производной функции \(f(x)\) в точке \(x_0\) .

Производная функции \(f(x)\) в точке \(x_0\) равна тангенсу угла наклона касательной к графику \(f(x)\) в точке \((x_0; f(x_0))\) (то есть угла между касательной к графику \(f(x)\) в точке \((x_0; f(x_0))\) и положительным направлением оси \(Ox\) ).

По рисунку видно, что касательная проходит через точки \((0,5; 0)\) и \((1; 1)\) , тогда тангенс угла наклона касательной составляет \(1 : 0,5 = 2\) , следовательно, \(f'(x_0) = 2\) .

Производная функции \(f(x)\) в точке \(x_0\) равна тангенсу угла наклона касательной к графику \(f(x)\) в точке \((x_0; f(x_0))\) .

По рисунку видно, что касательная проходит через точки \((0,5; -0,5)\) и \((1; 1)\) , тогда тангенс угла наклона касательной составляет \(1,5 : 0,5 = 3\) , следовательно, \(f'(x_0) = 3\) .

По рисунку видно, что касательная проходит через точки \((0,5; 1)\) и \((1,5; 1,5)\) , тогда тангенс угла наклона касательной составляет \(0,5 : 1 = 0,5\) , следовательно, \(f'(x_0) = 0,5\) .

По рисунку видно, что касательная проходит через точки \((1; 1)\) и \((5; 2)\) , тогда тангенс угла наклона касательной составляет \((2 - 1) : (5 - 1) = 0,25\) , следовательно, \(f'(x_0) = 0,25\) .

На рисунке изображен график функции \(y=f(x)\) и отмечены точки \(-2; \ 0; \ 2; \ 8\) . В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.

Проведем касательные к графику функции в этих точках. Так как тангенс угла \(\alpha\) наклона касательной равен значению производной \(f'(x)\) в точке касания \(x_0\) ( \(f'(x_0)=\mathrm\,\alpha\) ), то нужно сравнить тангенсы углов, отмеченных на рисунке.
Вспомним, что если угол тупой, то его тангенс отрицательный, если острый – положительный. Следовательно, так как мы ищем наибольший тангенс, имеет смысл рассматривать только острые углы. Это углы, образованные касательными в точках \(0\) и \(2\) . Заметим, что угол в точке \(0\) больше, следовательно, его тангенс также больше, чем тангенс угла в точке \(2\) . Таким образом, ответ: \(0\) .

Производная \(f'(x)\) функции \(f(x)\) в точке \(x_0\) равна \(10\) . Найдите котангенс угла наклона касательной к графику функции \(f(x)\) в точке \((x_0; f(x_0))\) .

При всех \(\alpha\) , при которых \(\mathrm\, \alpha\) и \(\mathrm\, \alpha\) имеют смысл, выполнено \(\mathrm\, \alpha\cdot\mathrm\, \alpha = 1\) , откуда котангенс угла наклона касательной к графику функции \(f(x)\) в точке \((x_0; f(x_0))\) равен \(0,1\) .

\(\blacktriangleright\) Если уравнение прямой задано в виде \(>\) , то число \(k\) называется угловым коэффициентом.

\(\blacktriangleright\) Угол \(\alpha\) наклона прямой – это угол между этой прямой и положительным направлением оси \(Ox\) ( \(0\leqslant \alpha< 180^\circ\) ), лежащий в верхней полуплоскости.

\(\blacktriangleright\) Основная формула. Угловой коэффициент прямой \(y=kx+b\) равен тангенсу угла наклона этой прямой:

\[<\large<\color\, \alpha>>>\]
Т.к. касательная к графику некоторой функции — это и есть прямая, то для нее верны все эти утверждения.

если \(\alpha>90^\circ\) , то \(k

если \(\alpha=0^\circ\) , то \(k=0\) (уравнение прямой имеет вид \(y=b\) и она параллельна оси \(Ox\) );

если \(\alpha=90^\circ\) , то уравнение прямой имеет вид \(x=a\) и она перпендикулярна оси \(Ox\) .

Прямая, заданная уравнением \(y = x\) , образует с положительным направлением оси \(Ox\) угол \(\alpha\) . Найдите \(\mathrm\, \alpha\) .

Для прямой, заданной уравнением \(y = kx + b\) , коэффициент \(k\) есть значение тангенса угла между прямой \(y = kx + b\) и положительным направлением оси \(Ox\) .

Так как для прямой \(y = x\) коэффициент \(k\) равен \(1\) , то \(\mathrm\, \alpha = 1\) .

Прямая, заданная уравнением \(y = 2x - 3\) , образует с положительным направлением оси \(Ox\) угол \(\alpha\) . Найдите \(\mathrm\, \alpha\) .

Так как для прямой \(y = 2x - 3\) коэффициент \(k\) равен \(2\) , то \(\mathrm\, \alpha = 2\) .

Прямая, заданная уравнением \(y = -x + 2\) , образует с положительным направлением оси \(Ox\) угол \(\alpha\) . Найдите \(\mathrm\, \alpha\) .

Так как для прямой \(y = -x + 2\) коэффициент \(k\) равен \(-1\) , то \(\mathrm\, \alpha = -1\) .

Прямая, заданная уравнением \(y = kx + 77\) , образует с положительным направлением оси \(Ox\) угол \(\alpha\) . Найдите \(k\) , если \(\mathrm\, \alpha = 12\) .

Так как тангенс угла \(\alpha\) между прямой \(y = kx + 77\) и положительным направлением оси \(Ox\) равен \(12\) , то \(k = \mathrm\, \alpha = 12\) .

Прямая, заданная уравнением \(y = kx + 0,2\) , образует с положительным направлением оси \(Ox\) угол \(\alpha\) . Найдите \(k\) , если \(\mathrm\, \alpha = -3,3\) .

Так как тангенс угла \(\alpha\) между прямой \(y = kx + 0,2\) и положительным направлением оси \(Ox\) равен \(-3,3\) , то \(k = \mathrm\, \alpha = -3,3\) .

Прямая, заданная уравнением \(y = kx\) , образует с положительным направлением оси \(Ox\) угол \(\alpha\) . Найдите \(k\) , если \(\mathrm\, \alpha = 0\) .

Так как тангенс угла \(\alpha\) между прямой \(y = kx\) и положительным направлением оси \(Ox\) равен \(0\) , то \(k = \mathrm\, \alpha = 0\) .

Прямая \(y = kx - 2016\) образует угол \(45^\) с положительным направлением оси \(Ox\) . Найдите \(k\) .

Так как угол между прямой \(y = kx - 2016\) и положительным направлением оси \(Ox\) равен \(\dfrac<\pi>\) , то \(k = \mathrm\, \dfrac<\pi> = 1\) .

Теме «Угловой коэффициент касательной как тангенс угла наклона» в аттестационном экзамене отводится сразу несколько заданий. В зависимости от их условия, от выпускника может требоваться как полный ответ, так и краткий. При подготовке к сдаче ЕГЭ по математике ученику обязательно стоит повторить задачи, в которых требуется вычислить угловой коэффициент касательной.

Сделать это вам поможет образовательный портал «Школково». Наши специалисты подготовили и представили теоретический и практический материал максимально доступно. Ознакомившись с ним, выпускники с любым уровнем подготовки смогут успешно решать задачи, связанные с производными, в которых требуется найти тангенс угла наклона касательной.

Основные моменты

Для нахождения правильного и рационального решения подобных заданий в ЕГЭ необходимо вспомнить базовое определение: производная представляет собой скорость изменения функции; она равна тангенсу угла наклона касательной, проведенной к графику функции в определенной точке. Не менее важно выполнить чертеж. Он позволит найти правильное решение задач ЕГЭ на производную, в которых требуется вычислить тангенс угла наклона касательной. Для наглядности лучше всего выполнить построение графика на плоскости ОХY.

Если вы уже ознакомились с базовым материалом на тему производной и готовы приступить к решению задач на вычисление тангенса угла наклона касательной, подобных заданиям ЕГЭ, сделать это можно в режиме онлайн. Для каждого задания, например, задач на тему «Связь производной со скоростью и ускорением тела», мы прописали правильный ответ и алгоритм решения. При этом учащиеся могут попрактиковаться в выполнении задач различного уровня сложности. В случае необходимости упражнение можно сохранить в разделе «Избранное», чтобы потом обсудить решение с преподавателем.

Значит, верна формула: \(f'(x_0)=\mathrm\, \alpha=k\) .

Производная \(f'(x)\) функции \(f(x)\) в точке \(x_0\) равна \(0\) . Найдите косинус угла наклона касательной к графику функции \(f(x)\) в точке \((x_0; f(x_0))\) .

Обозначим угол наклона касательной к графику функции \(f(x)\) в точке \((x_0; f(x_0))\) через \(\alpha\) . Так как \(\mathrm\, \alpha = \dfrac\) , то \(\sin \alpha = 0\) , откуда при помощи основного тригонометрического тождества находим, что \(\cos \alpha = \pm 1\) .

Так как \(\alpha\) – угол между двумя прямыми, то \(0^ \leq \alpha < 180^\) , тогда \(\cos \alpha\) не может быть равен \(-1\) , следовательно, \(\cos \alpha = 1\) .

Производная \(f'(x)\) функции \(f(x)\) в точке \(x_0\) равна \(\dfrac>\) . Найдите синус угла наклона касательной к графику функции \(f(x)\) в точке \((x_0; f(x_0))\) .

Обозначим угол наклона касательной к графику функции \(f(x)\) в точке \((x_0; f(x_0))\) через \(\alpha\) , тогда \(\mathrm\, \alpha = \dfrac>\) , причём \(0^ \leq \alpha < 180^\) .

(тут \(\cos \alpha > 0\) так как при \(0^ \leq \alpha < 180^\) \(\sin \alpha \geq 0\) и получается, что левая часть равенства положительна, числитель правой части неотрицателен, тогда знаменатель правой части положителен).

Решая уравнение \(\dfrac> = \dfrac>\) , находим \(\sin \alpha = \pm 0,25\) , но так как \(0^ \leq \alpha < 180^\) , то \(\sin \alpha = 0,25\) .

Найдите тангенс угла наклона касательной к графику функции \(y = 2(\ln 2)^\cdot e^\) в точке с абсциссой \(x = \sqrt<\ln 2>\) .

Тангенс угла наклона касательной к графику функции \(y = f(x)\) в точке с абсциссой \(x\) равен \(f'(x)\) . \[y' = 2(\ln 2)^\cdot 2x\cdot e^\,,\] тогда при \(x = \sqrt<\ln 2>\) имеем: \[y'(\sqrt<\ln 2>) = 2(\ln 2)^\cdot 2\sqrt<\ln 2>\cdot e^ <\ln 2>= 8\,.\]

Какой наибольший угол может составлять касательная к графику функции \(y = 2\sin \left(\dfrac>x\right)\) с графиком функции \(y = 0\) ? Ответ дайте в градусах.

Обозначим угол между касательной к графику функции \(y = 2\sin \left(\dfrac>x\right)\) в точке с абсциссой \(x_0\) и прямой \(y = 0\) через \(\alpha(x_0)\) , а угол наклона касательной к графику этой же функции в той же точке через \(\beta(x_0)\) . Тогда \(\alpha(x_0) = \) меньшему из углов \(\beta(x_0)\) и \(180^\circ - \beta(x_0)\) , следовательно,

\[\left[ \begin \begin &\mathrm\,(\alpha(x_0)) = \mathrm\,(\beta(x_0))\\ &\mathrm\,(\alpha(x_0)) = \mathrm\,(180^\circ - \beta(x_0)) = -\mathrm\,(\beta(x_0)) \end \end \right.\]

Но \(\alpha(x_0)\in[0; 90^\circ]\) , тогда \(\mathrm\,(\alpha(x_0))\geqslant 0\) и чем больше \(\mathrm\,(\alpha(x_0))\) , тем больше \(\alpha(x_0)\) .

Так как \(f'(x_0)\) – тангенс угла наклона касательной к графику функции \(y = f(x)\) в точке \((x_0; f(x_0))\) , то \[\mathrm\,(\beta(x_0)) = y'(x_0) = \sqrt\cdot \cos \left(\dfrac<\sqrt>x_0\right)\]

Если \(\mathrm\,(\alpha(x_0)) = \mathrm\,(\beta(x_0))\) , то наибольшее значение \(\mathrm\,(\alpha(x_0))\) равно \(\sqrt\) . Если \(\mathrm\,(\alpha(x_0)) = -\mathrm\,(\beta(x_0))\) , то наибольшее значение \(\mathrm\,(\alpha(x_0))\) тоже равно \(\sqrt\) . Тогда наибольшее значение \(\alpha\) равно \(\mathrm\, \sqrt\) .

Читайте также: