Центр масс холодильника находится на высоте h от пола посередине между опорами

Обновлено: 23.04.2024

Лестница - стремянка состоит из двух половинок одинаковых по размерам, но разных по массе. Лестницу ставят на горизонтальный пол. На какой максимальный угол можно раздвинуть половинки, если коэффициент их трения о пол равен 0,5? Массы половинок равны 3m и m. (≈ 73,8º)

Проволочный прямоугольный треугольник с углом  = 30º поставлен вертикально. По катетам треугольника без трения могут скользить две бусинки связанные нитью (рис. 11.34). Массы бусинок равны m₁ = 100 г и m₂ = 300 г. Определить силу натяжения нити и угол  в положении равновесия. Будет ли положение равновесия устойчивым? ( 79º;  2,65 Н; будет)

Две гладкие наклонные плоскости наклонены под углами 30º и 60º к горизонту и составляют двугранный угол. В этот угол кладут гладкий однородный стержень (рис. 11.35). Какой угол будет составлять стержень с горизонтом в положении равновесия? Будет ли положение равновесия устойчивым? (30º; не будет)

Д иск насажен на горизонтальный вал. Радиус диска равен 20 см, а радиус вала – 2 см. Для того, чтобы стащить диск с вала, его нужно тянуть с силой 100 Н. Для облегчения этой операции к ободу диска прикладывают касательную силу 8 Н и одновременно тянут его с силой F. При каком значении F диск начнет сниматься с вала? (60 Н)

Два одинаковых тяжелых ящика лежат на полу. Их пытаются сдвинуть с места, вставив между ними лом (рис. 11.36). Какой из ящиков сдвинется раньше? (Правый)

Невесомый стержень длиной l вращается с постоянной скоростью вокруг вертикальной оси О, проходящей через один из его концов. На другом конце стержня укреплен диск, который катится по горизонтальной поверхности (рис. 11.37). Масса диска m, коэффициент трения между диском и поверхностью . Найти момент силы на оси О. Ось диска составляет угол  со стержнем.

Т ележка приводится в движение пружиной как показано на рисунке. В начальном состоянии тележка удерживается нитью, а пружина растянута силой F. Точка крепления пружины к колесу находится на расстоянии l над центром колеса (рис. 11.38). Радиус колеса тележки равен R, а масса тележки - m. С каким ускорением начнет двигаться тележка, если перерезать нить? Массой колес пренебречь. Считать, что колеса не проскальзывают.

Однородный прямоугольный ящик лежит на гладкой горизонтальной поверхности на двух опорах. Ящик начинают тянуть горизонтальной силой, приложенной в точке А. Какая из опор при этом сильнее давит на поверхность? А если сила приложена в точке В (рис. 11.39)? (Правая; левая)

В предыдущей задаче высота ящика равна а, длина - b, а масса - m. Горизонтальную силу прикладывают сначала в точке А, а затем в точке В. При каком значении силы одна из опор оторвется от поверхности?

Автомобиль имеет две оси, расстояние между которыми равно l. Центр масс автомобиля расположен посередине между осями и на высоте h над землей. Какое максимальное ускорение может развить автомобиль, если ведущая ось: а) задняя; б) передняя? Коэффициент трения между колесами и дорогой равен , размерами и массой колес пренебречь.

Автомобиль массой М поднимается с постоянной скоростью вверх по дороге, образующей угол  с горизонтом. Найти силу взаимодействия ведущих (задних) колес с дорогой. Расстояние между осями колес автомобиля L, центр масс находится посередине между осями колес и на высоте h. На передние колеса сила трения не действует.

Какой максимальной длины доску можно забить между двумя вертикальными стенами. Расстояние между стенами равно l, коэффициент трения между ними и доской равен , массой доски пренебречь (рис. 11.40).

Я щик размерами a  b стоит с одной стороны на колесиках, а с другой - на жестком упоре. Ящик ставят на наклонную плоскость колесиками вниз (рис. 11.41). При этом он начинает скатываться, когда угол наклона плоскости равен  = 15º. При каком угле наклона начнет скатываться ящик, если его поставят на наклонную плоскость колесиками вверх? Принять b = 2a. Размерами колес и упора пренебречь.

Кубик стоит наклонно в углу комнаты (рис. 11.42). При каком наименьшем значении угла  возможно такое равновесие, если коэффициент трения везде одинаков и равен ?

Два одинаковых однородных стержня соединены шарнирно и лежат на гладком горизонтальном цилиндре, радиус которого равен R (рис. 11.43). В положении равновесия угол между стержнями равен 90º. Какова длина стержней? Устойчиво ли такое положение равновесия? (L = 4R; устойчиво)

Г оризонтальная доска имеет ступеньку высотой Н, в которую упирается свободно лежащий на доске однородный цилиндр радиуса R > H. Доску двигают горизонтально с ускорением а. Определить максимально возможное ускорение а_max, при котором цилиндр еще не будет подниматься на ступеньку. Трением пренебречь.

Три одинаковых цилиндра сложены вместе и находятся между двумя вертикальными стенами, удерживаясь силами трения (рис. 11.44). Считая коэффициент трения везде одинаковым, найти при каком минимальном значении коэффициента трения возможно такое равновесие?

Т ри одинаковых бревна сложены вместе и лежат на горизонтальной поверхности как показано на рис. 11.45. При каком коэффициенте трения это возможно, считая его везде одинаковым.

Невесомый обруч, к которому прикреплен небольшой грузик, стоит на доске, движущейся с горизонтальным ускорением а (рис. 11.46). Угол  известен и постоянен. Найти ускорение. Обруч по доске не скользит.

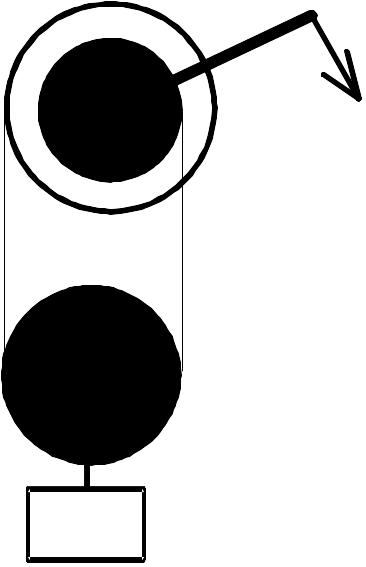
Н еоднородный стержень висит на двух нитях как показано на рис. 11.47. Построением найти центр тяжести стержня.

Какой груз можно поднять с помощью дифференциального ворота, прикладывая к рукоятке силу 2,5 Н? Длина рукоятки равна 1 м, радиус большого цилиндра - 20 см, радиус малого - 10 см, момент силы трения на оси ворота составляет 20% от момента приложенной силы. (40 Н)

Стержень, шарнирно прикрепленный к полу, опирается на лежащий на полу цилиндр (рис. 11.48). При каком максимальном значении угла наклона стержня возможно равновесие системы, если коэффициент трения между стержнем и цилиндром равен . Трение между цилиндром и полом велико.

З аторможенный блок, через который перекинута нить с грузами массой m₁ и m₂ на концах, уравновешен на равноплечных весах (рис. 11.49). На сколько следует изменить массу гирь на другой чашке весов, чтобы равновесие сохранилось после освобождения блока?

Невесомые стержни АВ и ВС соединены шарнирно между собой и с вертикальной стенкой. Угол между стержнями равен . К середине стержня АВ подвешен груз массой m (рис. 11.50). Определить силы давления стержня АВ на шарниры А и В.

Невесомый стержень АВ шарнирно прикреплен к стене в точке А и удерживается под углом 45° к стене горизонтальной растяжкой ВС (рис. 11.51). В точках B и D к стержню через неподвижный блок подвешен груз массой m (точка D - середина стержня). Найти силу натяжения растяжки ВС и силу реакции в шарнире. (T = 0,75mg; F = 1,25mg)

В стену на одной вертикальной линии вбито два гвоздя. На них вешают тонкий обруч массой m, как показано на рис. 11.52. С какой силой обруч давит на гвозди, если расстояние между гвоздями равно радиусу обруча? ( )

Какой минимальной силой можно опрокинуть через ребро однородный куб массой m, лежащий на горизонтальной поверхности? Каким должен быть при этом коэффициент трения куба о поверхность?

Однородный шарнирно закрепленный стержень удерживается под углом 45 0 к горизонту горизонтальной нитью, перекинутой через неподвижный блок. Для удержания стержня в таком положении на другой конец нити надо повесить груз массой m. Какой груз должен висеть на нити, чтобы удержать стержень в горизонтальном положении? Шарнир и ось блока находятся на одной вертикали. ( )

Однородная тонкая пластинка имеет форму треугольника со сторонами 13 см, 14 см, 15 см. На каком расстоянии от второй стороны находится центр тяжести пластинки? (4 см)

Каким должен быть минимальный коэффициент трения, чтобы клин, заколоченный в бревно, не выскакивал из него? Угол при вершине клина  = 30°. ( 0,27)

Гладкий стержень согнут в виде угла  и расположен так, что биссектриса угла вертикальна. На угол надели петлю из легкой нити, на которой закреплен небольшой груз (рис. 11.53). Определить угол , который образует нить, отходящая от груза, в положении равновесия.

К атушку тянут за нитку, пропущенную в отверстие стола (рис. 11 54). При каком значении коэффициента трения катушка будет проворачиваться на месте. Радиусы катушки R и r. Массой катушки пренебречь.

На внутренней поверхности гладкой сферы лежит невесомый стержень с маленькими шариками массами m₁ и m₂ на концах (рис. 11.55). Длина стержня равна радиусу сферы. Найти угол между стержнем и горизонталью.

Однородная пластина имеет форму круга радиусом R. В пластине вырезано отверстие радиусом R/2, касающееся края пластины. Пластину поставили вертикально на горизонтальную поверхность. Какую вертикальную силу в точке касания надо приложить к пластине, чтобы центры пластины и отверстия находились на одном горизонтальном уровне (рис. 11.56)? Масса пластины с вырезом равна m.

Тонкий однородный диск радиусом R подвешен на двух нитях, как показано на рис. 11.57. В диске вырезано отверстие радиусом R/2, касающееся края диска. Найти силы натяжения нитей, если толщина диска равна h, а плотность материала диска ρ.

Шар радиусом R и массой m движется поступательно по горизонтальной поверхности под действием постоянной силы натяжения нити F. Точка закрепления нити находится на высоте h (рис. 11.58). Чему равно ускорение шара?

Прямоугольный брусок с размерами а х b равномерно тянут по горизонтальной поверхности за веревку, угол наклона которой может меняться. Коэффициент трения равен . При каком угле наклона  брусок начнет приподниматься?

Вертушка состоит из трех легких одинаковых стержней, скрепленных в одной точке. Углы между стержнями одинаковы. На свободных концах стержней закреплены маленькие шарики массами m, 2m и 3m. Вертушка может свободно вращаться вокруг горизонтальной оси, проходящей через точку скрепления стержней. Чему равен угол α в положении равновесия системы. (30º)

Разделы

Дополнительно

Задача по физике - 8828

Где расположен центр тяжести двух частей разрезанной тонкой сферы радиусом $R$, лежащих на полу одна на другой (рис.)?

Задача по физике - 8829

Определите положение центра тяжести замкнутой фигуры из однородной проволоки, сделанной в виде полукольца радиусом $R$ (рис.).

Задача по физике - 8830

Где находится центр тяжести палки длиной $l$, согнутой под прямым углом в отношении 1 : 4?

Задача по физике - 8831

Треугольная призма массой $m$ состоит из двух одинаковых половинок. Основание призмы представляет собой равносторонний треугольник. Стоя на одном ребре, призма находится в состоянии неустойчивого равновесия. Половинки призмы стянуты нитью АВ (рис.). Какова должна быть минимальная сила натяжения нити, чтобы призма не распалась?

Задача по физике - 8832

Два человека несут бревно, диаметр которого изменяется от $d_<1>$ до $d_$. Длина бревна $l$. На каком расстоянии от тонкого конца должен взяться за бревно второй человек, чтобы оба несущих испытывали одинаковую нагрузку, если первый держится за толстый край?

Задача по физике - 8833

Два стержня, одинаковые по форме и размерам, но сделанные из разных материалов с модулями Юнга $E_<1>$ и $E_$, склеены торцами. Какой модуль Юнга $E$ должен иметь материал, чтобы изготовленный из него стержень проявлял те же упругие свойства, что и система двух стержней?

Задача по физике - 9293

Однородная нить массы $m$ свободно висит так, что оба ее конца закреплены и находятся на одной высоте. Сила натяжения нити в нижней точке равна $T_<0>$. Найти силу натяжения нити вблизи точек подвеса.

Задача по физике - 9296

Чтобы сдвинуть контейнер влево, к центру его правой стороны, перпендикулярно ей, необходимо приложить силу $F_ <1>= 10^ Н$, а чтобы сдвинуть его вправо, нужно приложить к центру левой стороны, перпендикулярно ей, силу $F_ = 1,5 \cdot 10^ Н$ (рис.). Найти массу контейнера. Левые опоры, в отличие от правых, сделаны на роликах, обеспечивающих пренебрежимо малое трение. Размеры опор малы. Контейнер считать однородным кубом.

Задача по физике - 9301

Небольшой груз массы $m$ закреплен посередине невесомой тележки высоты $h$. Расстояния от него до обеих осей тележки равны $l$. Тележка катится по наклонной плоскости с углом при основании $\alpha$ (рис.). В некоторый момент с помощью тормозных колодок мгновенно останавливают вращение колес тележки. Коэффициент трения скольжения передних колес о плоскость равен $k_<1>$, задних — $k_$. При каком угле а тележка начнет двигаться равномерно?

Задача по физике - 9302

У стенки, прижимаясь к ней, лежит катушка массы $m$ радиуса $2R$, на внутренний цилиндр которой намотана нить (рис.). За нить тянут вертикально вниз. При каком значении силы натяжения нити $F$ катушка начнет вращаться? Коэффициенты трения о пол и стенку одинаковы и равны $k$, радиус внутреннего цилиндра равен $R$.

Задача по физике - 9303

На горизонтальном столе находится лист бумаги, прижатый однородным стержнем массы $m$, верхний конец которого шарнирно закреплен. Какую минимальную горизонтальную силу необходимо приложить к листу, чтобы вытащить его? Угол между стержнем и листом равен $\alpha$, коэффициент трения между ними равен $k$. Трением между столом и бумагой пренебречь.

Задача по физике - 9304

Жесткий стержень длины $l$ может свободно поворачиваться вокруг оси О, закрепленной на расстоянии $l$ от гладкой вертикальной стенки (рис.). Между стержнем и стенкой зажат брусок толщины $h$. При какой толщине бруска его невозможно протянуть вниз, если коэффициент трения между стержнем и бруском равен $k$.

Задача по физике - 9305

Брусок длины $l$ и массы $m$ подвешен на двух параллельных невесомых жестких стержнях, соединенных шарниром с перекладиной длины $L$, стоящей на опорах (рис.). Правый стержень находится на расстоянии $d$ от правого конца перекладины. Брусок начинает движение из наивысшего положения без начальной скорости. Найти максимальную разность сил, действующих на правую и левую опоры перекладины. Прогибом перекладины и трением пренебречь.

Задача по физике - 9311

Одна из стенок прямоугольного сосуда с водой образована бруском. Брусок представляет собой призму, в плоскостях боковых сторон сосуда имеющую сечение в виде равнобедренного прямоугольного треугольника, и может перемещаться по дну сосуда (рис.). Считая, что трение между бруском и боковыми стенками отсутствует, найти минимальный коэффициент трения между основанием сосуда и бруском, при котором брусок придет в движение. Длина бруска $l = 20 см$, его масса $m = 90 г$, угол при вершине призмы $\alpha = 45^< \circ>$, высота столба воды $h = 1 см$, плотность воды $\rho_ <0>= 1 \cdot 10^ кг/м^$.

Задача по физике - 9342

Бревно уравновешено на тросе (рис.). Докажите, что если распилить бревно по линии обхвата троса, то конец АС окажется тяжелее конца СВ.

2017-03-08
Определите максимальное ускорение, с которым заднеприводный автомобиль с расстоянием между осями $L=1,2 м$, центр тяжести которого расположен на высоте $h=1 м$ от земли посередине между осями, может начать двигаться, если он находится а) на льду, б) на асфальте. Коэффициент трения скольжения колес по льду 0,1; по асфальту 0,7.

На автомобиль действуют сила тяжести $M \vec$, приложенная к его центру масс, и силы реакции опоры на передние и задние колеса $\vec_$ и $\vec_$ соответственно (рис.). Кроме того, на задние колеса действует сила трения $\vec_$, являющаяся силой трения покоя и направленная по направлению движения автомобиля (это становится очевидным, если заметить, что нижняя точка колеса неподвижна относительно земли, а действующий на колесо со стороны двигателя момент сил стремится сдвинуть ее против направления движения автомобиля). Именно эта сила трения покоя и движет автомобиль вперед. В то же время на переднее колесо не действуют ни сила трения покоя, ни сила трения скольжения, т.к. оно катится без проскальзывания и не приводится во вращение мотором.

Записав второй закон Ньютона в проекциях на вертикальную и горизонтальную ось и уравнение моментов относительно т.А, являющейся точкой пересечения проведенной через центр тяжести горизонтали и проведенной через ось заднего колеса вертикали (см. рис. 34), получим систему уравнений, описывающую движение автомобиля:

$\begin F_ = Ma_ \\ N_ + N_ = Mg \\ N_ L + F_ h = Mg \frac \end$ (1)

Учитывая, что сила трения покоя $F_ \leq \mu N_$, можно прийти к системе неравенств, ограничивающих значение ускорения:

$\begin a \leq \mu \frac> \\ a \leq \left ( \frac> - \frac \right ) \frac \end$ (2)

При нарушении первого условия системы (2) задние колеса начнут проскальзывать, а при нарушении второго условия нарушится третье уравнение системы (1), суммарный момент сил $\vec_$ и $\vec_$ превысит момент силы тяжести и автомобиль опрокинется назад.

Поскольку правые части неравенств системы (2) прямо пропорциональны силе $N_$, то максимальное ускорение достигается при ее максимальном значении. Очевидно, что оно равно значению силы тяжести, тогда (2) принимает вид

$\begin a \leq \mu g \\ a \leq \frac g \end$. (2)

Непосредственным вычислением несложно убедиться, что при $\mu = 0,1$ существенным оказывается первое неравенство, а при $\mu = 0,7$ - второе.
Ответ: а)$1 м/с^$, б) $6 м/с^$.

Разделы

Дополнительно

Задача по физике - 5218

Из центра пола цилиндрической комнаты под углом $\alpha$ к горизонту с некоторой скоростью бросают мячик. Через время $T$, после трёх упругих ударов о стенки и потолок, он опять оказывается в центре пола. Определите скорость мячика при броске. Радиус комнаты равен $r$. Сопротивлением воздуха пренебречь. Ускорение свободного падения равно $g$.

Задача по физике - 5219

Горит башня, причём возгорание произошло в двух местах: на 1/10 высоты башни и на $L = 220 м$ выше. Пламя распространяется вверх в $s = 7$ раз быстрее, чем вниз. Башня сгорела дотла за $t_ <1>= 60 ч$. Если бы $L$ было в 2 раза больше, башня сгорела бы целиком за $t_ = 61 ч$, а если бы в 2 раза меньше, то время бы не изменилось (60 ч). Чему была равна высота башни?

Задача по физике - 5220

Вдоль бесконечно длинной дороги стоят светофоры, отделённые друг от друга одинаковыми расстояниями $L$. На каждом светофоре периодически включается на некоторое время красный свет, а затем, на то же самое время, включается зелёный, причём, на каждом следующем светофоре красный свет включается в тот момент, когда на предыдущем включается зелёный. Найти все возможные периоды работы светофоров (время от одного включения красного света до следующего на данном светофоре), при которых возможно равномерное безостановочное движение машин со скоростью $V$.

Задача по физике - 5221

Вдоль бесконечно длинной дороги стоят шлагбаумы, отделённые друг от друга одинаковыми расстояниями. Каждый шлагбаум периодически открывается на период $T_ <1>= 1,1 \tau$, а затем закрывается на время $T_ = 0,9 \tau$, причём, каждый последующий шлагбаум открывается через некоторое, одинаковое для всех шлагбаумов, время после предыдущего. При каких расстояниях между шлагбаумами возможно равномерное безостановочное движение машин со скоростью $V$ в обе стороны? Как изменится ответ, если $T_ = 1,1 \tau$,а $T_ <1>= 0,9 \tau$?

Задача по физике - 5222

В мензурке достаточной высоты упруго скачет большое количество шариков. Каждый из них долетает ровно до отметки 750 мл. В некоторый момент мензурку начинают опускать вниз с ускорением $g/2$. Какая часть шариков после этого будет долетать до отметки 1 литр? Шарики не сталкиваются друг с другом и ударяются о дно мензурки в случайные моменты времени. Мензурка имеет цилиндрическую форму.

Задача по физике - 5223

Маленькая монета находится внутри тазика, сечение которого показано на рис. На какой высоте относительно дна тазика будет находиться монета, если тазик не наклоняя двигать с горизонтальным ускорением 20 $м/с^<2>$? Сухим трением монеты о тазик можно пренебречь.

Задача по физике - 5224

В комнате висит герметичный пакет, наполненный лёгким газом и прикреплённый к полу верёвкой. Как изменится высота пакета над полом, если воздух в комнате нагреть? Ответ обоснуйте.

Задача по физике - 5225

Машина массы $m$ стоит на горизонтальном покрытии с коэффициентом трения $\mu$. Двигатель машины развивает постоянную мощность $P$, передаваемую на задние колёса машины. Какой путь пройдёт машина при старте с места до окончания пробуксовки колёс? Центр масс машины всегда расположен посередине между передней и задней осью на высоте $h$ от поверхности дороги. Расстояние между осями $L$. Автомобиль разгоняется по прямой с постоянным ускорением, его передние колёса не отрываются от поверхности.

Задача по физике - 5226

На длинный горизонтальный стержень надеты $N$ одинаковых неупругих бусинок (см. рис.). С краю находится ещё одна бусинка в 2 раза большей массы. Ей придают некоторую скорость в направлении остальных бусинок, сообщая кинетическую энергию $E$. Найдите выделившееся в результате соударений тепло. Трением пренебречь.

Задача по физике - 5227

Было решено построить глубоководную лабораторию. Для этого под воду опускают лёгкие модули объёма $V$ с помощью прикреплённого к ним балласта массы $M$. После этого модули закрепляют на дне, а балласт медленно поднимают на борт судна (см. рис.). Каков КПД описанного способа погружения? Плотность вещества балласта $\rho$, плотность воды $\rho_<0>$, ускорение свободного падения $g$. Размеры модуля и балласта малы по сравнению с глубиной их погружения.

Задача по физике - 5228

На краю доски длиной $L$ лежит кусочек резины. Коэффициент трения покоя между резиной и доской равен $m_<1>$, коэффициент трения скольжения равен $m_$. Конец доски, на котором лежит резинка, начинают медленно поднимать, и в некоторый момент она соскальзывает. После начала её движения угол между доской и горизонтом не меняется. За какое время резинка достигнет другого края доски? Ускорение свободного падения равно $g$.

Задача по физике - 5229

Автомобиль двигается вниз по склону с постоянным ускорением $a = 1 м/с^<2>$. Каким должен быть коэффициент трения, чтобы это было возможно? Уклон горы $\alpha = 45^< \circ>$.

Задача по физике - 5230

Известно, что разгоняя поезд из состояния покоя с ускорением $a$, электровоз совершает работу $A$. Чему окажется равна эта работа, если за время разгона грузчики перенесут из заднего вагона в передний груз массой $m$? Массу грузчиков не учитывать. Расстояние между первым и последним вагоном равно $L$.

Задача по физике - 5231

Небольшое тело массы $m$ устанавливают в верхней точке наклонной плоскости высоты $h$ и сообщают ему начальную скорость $V_<0>$, направленную вдоль наклонной плоскости. Поверхность плоскости неоднородна, поэтому скорость тела изменяется произвольным образом. В нижней точке плоскости скорость тела также равна $V_<0>$. Найти работу силы трения.

Задача по физике - 5232

Для тренировки космонавтов используется имитатор невесомости. Космонавт крепится к легкому тонкому тросу, намотанному на лёгкий барабан радиуса $r_<1>$. На барабане имеется тормозное устройство в виде цилиндра радиуса $r_$, к которому могут с силой $F$ прижиматься тормозные колодки. Коэффициент трения между колодками и барабаном $\mu$. В процессе тренировки космонавт свободно падает с нулевой начальной скоростью время $T$, затем включается тормоз, и космонавт достигает земли с нулевой скоростью. Какова должна быть минимальная высота начальной точки полёта? Ускорение свободного падения равно $g$.

Черноуцан А. Задачи на центр масс // Квант. — 1996. — № 2. — С. 43-45.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

При решении механических задач неоценимую помощь может оказать использование понятия центра масс системы материальных точек. Одни задачи просто невозможно решить, не прибегая к этому понятию, решение других с его помощью может стать гораздо проще и нагляднее.

Перед тем как обсуждать конкретные задачи, напомним основные свойства центра масс и проиллюстрируем их примерами.

Центром масс (центром инерции) системы материальных точек назовем точку, характеризующую распределение масс в системе, координаты которой определяются формулами

Пример 1. Найдем положение центра масс, простейшей системы, состоящей из двух точек, массы которых m₁ и m₂ и расстояние между ними l (рис. 1).

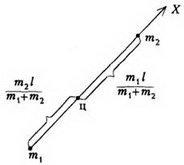
Направив ось X от первой точки ко второй, получим, что расстояние от первой точки до центра масс (т.е. координата центра масс) равно а расстояние от центра масс до второй точки равно т.е. отношение расстояний обратно отношению масс. Значит, в этом случае положение центра масс совпадает с центром тяжести.

Обсудим некоторые свойства центра масс, что, как нам кажется, наполнит физическим содержанием приведенное выше несколько формальное определение этого понятия.

1) Положение центра масс не изменится, если какую-то часть системы заменить одной точкой с массой, равной массе этой подсистемы, и находящейся в ее центре масс.

Пример 2. Рассмотрим плоский однородный треугольник и найдем положение его центра масс. Разделим треугольник на тонкие полоски, параллельные одной из сторон, и заменим каждую полоску точкой, расположенной в ее середине. Так как все такие точки лежат на медиане треугольника, центр масс тоже должен лежать на медиане. Повторяя рассуждения для каждой из сторон, получаем, что центр масс находится на пересечении медиан.

2) Скорость центра масс можно найти, взяв производную по времени от обеих частей равенства (1):

где — импульс системы, m — полная масса системы. Видно, что скорость центра масс замкнутой системы постоянна. Значит, если связать с центром масс поступательно движущуюся систему отсчета, то она будет инерциальной.

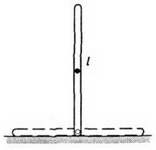
Пример 3. Поставим однородный стержень длиной l вертикально на гладкую плоскость (рис. 2) и отпустим. В процессе падения как горизонтальная составляющая его импульса, так и горизонтальная составляющая скорости центра масс будут оставаться равными нулю. Поэтому в момент падения центр стержня окажется в том месте, где первоначально стоял стержень, а концы стержня сместятся по горизонтали на .

3) Ускорение центра масс равно производной от его скорости по времени:

где в правой части равенства стоят только внешние силы, так как все внутренние силы сокращаются по третьему закону Ньютона. Получаем, что центр масс, движется так, как двигалась бы воображаемая точка с массой, равной массе системы, под действием результирующей внешней силы. Наверное, это самое физическое свойство центра масс.

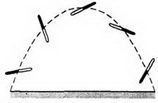
Пример 4. Если бросить палку, приведя ее при этом во вращение, то центр масс палки (ее середина) будет двигаться с постоянным ускорением по параболе (рис. 3).

4) Пусть система точек находится в однородном поле тяжести. Тогда суммарный момент сил тяжести относительно любой оси, проходящей через центр масс, равен нулю. Это значит, что равнодействующая сил тяжести проходит через центр масс, т.е. центр масс является также центром тяжести.

5) Потенциальная энергия системы точек в однородном поле тяжести вычисляется по формуле

где h_ц — высота центра масс системы.

Пример 5. При выкапывании в однородном фунте ямы глубиной h и разбрасывании грунта по поверхности его потенциальная энергия возрастает на , где m — масса извлеченного грунта.

6) И еще одно полезное свойство центра масс. Кинетическая энергия системы точек может быть представлена в виде суммы двух слагаемых: кинетической энергии общего поступательного движения системы, равной , и кинетической энергии E_отн движения относительно системы отсчета, связанной с центром масс:

Пример 6. Кинетическая энергия обруча, катящегося без проскальзывания по горизонтальной поверхности со скоростью υ, равна

так как относительное движение в этом случае представляет собой чистое вращение, для которого линейная скорость точек обруча равна υ (полная скорость нижней точки должна быть равна нулю).

Теперь приступим к разбору задач на использование центра масс.

Задача 1. Однородный стержень лежит на гладкой горизонтальной поверхности. К стержню прикладывают две одинаковые по величине, но противоположные по направлению горизонтальные силы: одна сила приложена к середине стержня, другая — к его концу (рис. 4). Относительно какой точки начнет поворачиваться стержень?

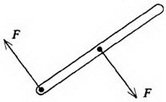
На первый взгляд может показаться, что осью вращения будет точка, лежащая посередине между точками приложения сил. Однако уравнение (3) показывает, что поскольку сумма внешних сил равна нулю, то равно нулю и ускорение центра масс. Значит, центр стержня будет оставаться в покое, т.е. служить осью вращения.

Задача 2. Тонкий однородный стержень длиной l и массой m привели в движение вдоль гладкой горизонтальной поверхности так, что он движется поступательно и одновременно вращается с угловой скоростью ω. Найдите, натяжение стержня в зависимости от расстояния x до его центра.

Перейдем в инерциальную систему отсчета, связанную с центром стержня. Рассмотрим движение куска стержня, заключенного между рассматриваемой точкой стержня (расположенной на расстоянии x от центра) и его концом (рис. 5).

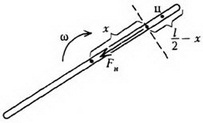
Единственной внешней силой для этого куска является искомая сила натяжения F_н, масса равна , а его центр масс движется по окружности радиусом с ускорением . Записывая уравнение движения центра масс выделенного куска, получим

Задача 3. Двойная звезда состоит из двух звезд-компонентов массами m₁ и m₂, расстояние между которыми не меняется и остается равным L. Найдите период вращения двойной звезды.

Рассмотрим движение звезд-компонентов в инерциальной системе отсчета, связанной с центром масс двойной звезды. В этой системе отсчета звезды движутся с одной и той же угловой скоростью по окружностям разных радиусов (рис. 6).

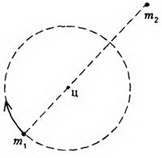
Радиус вращения звезды массой m₁ равен (см. Пример 1), а ее центростремительное ускорение создается силой притяжения к другой звезде:

Видим, что период вращения двойной звезды равен

и определяется полной массой двойной звезды, независимо от того, как она распределена между звездами-компонентами.

Задача 4. Две точечные массы m и 2m связаны невесомой нитью длиной l и движутся по гладкой горизонтальной плоскости. В некоторый момент времени скорость массы 2m равна нулю, а скорость массы m равна υ и направлена перпендикулярно нити (рис. 7). Найдите натяжение нити и период вращения системы.

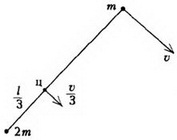
Центр масс системы находится на расстоянии от массы 2m и движется со скоростью . В системе отсчета, связанной с центром масс, точка массой 2m движется по окружности радиусом со скоростью . Значит, период вращения равен (проверьте, что такой же ответ получается, если рассмотреть точку массой m). Натяжение нити найдем из уравнения движения любой из двух точек:

Задача 5. На гладкой горизонтальной плоскости лежат два одинаковых бруска массой m каждый, связанных легкой пружиной жесткостью k (рис. 8). Первому бруску сообщают скорость υ₀ в направлении от второго бруска. Опишите движение системы. Через какое время деформация пружины впервые достигнет максимального значения?

Центр масс системы будет перемещаться с постоянной скоростью . В системе отсчета центра масс начальная скорость каждого бруска равна , а жесткость половинной пружины, которая соединяет его с неподвижным центром масс, составляет 2k (жесткость пружины обратно пропорциональна ее длине). Период таких колебаний равен

а амплитуда колебаний каждого бруска, которую можно найти из закона сохранения энергии, составляет

В первый раз деформация станет максимальной через четверть периода, т.е. через время .

Задача 6. Шар массой m налетает со скоростью υ на покоящийся шар массой 2m. Найдите скорости обоих шаров после упругого центрального удара.

В системе отсчета, связанной с центром масс, полный импульс двух шаров равен нулю как до, так и после coyдарения. Легко догадаться, какой ответ для конечных скоростей удовлетворяет одновременно и этому условию, и закону сохранения энергии: скорости останутся такими же, как до удара, по величине, но изменят свои направления на противоположные. Скорость центра масс системы равна . В системе центра масс первый шар движется со скоростью , а второй шар движется навстречу первому со скоростью . После удара шары будут разлетаться с такими же скоростями. Осталось вернуться в первоначальную систему отсчета. Применяя закон сложения скоростей, находим, что конечная скорость шара массой m равна и направлена назад, а скорость покоившегося раньше шара массой 2m равна и направлена вперед.

Отметим, что в системе центра масс очевидным является утверждение, что при ударе относительная скорость шаров не меняется по величине, но меняется по направлению. А так как разность скоростей при переходе в другую инерциальную систему отсчета не изменяется, можно считать, что мы вывели это важное соотношение и для первоначальной системы отсчета:

где буква υ используется для обозначения начальных скоростей, а u — для конечных. Это уравнение можно решать совместно с законом сохранения импульса вместо закона сохранения энергии (куда скорости входят во второй степени).

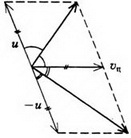
Задача 7. Известно, что при упругом нецентральном ударе двух одинаковых шаров, один из которых до удара покоился, угол разлета равен 90°. Докажите это утверждение.

В системе центра масс нецентральный удар можно описать следующим образом. До удара шары сближаются с одинаковыми импульсами, после удара они разлетаются с такими же по величине, но противоположно направленными импульсами, а прямая разлета поворачивается на некоторый угол относительно прямой сближения. Чтобы перейти обратно в начальную систему отсчета, надо каждую конечную скорость сложить (векторно!) со скоростью центра масс. В случае одинаковых шаров скорость центра масс равна , где υ — скорость налетающего шара, и в системе отсчета центра масс шары сближаются и разлетаются с одинаковыми скоростями . В том, что после сложения каждой конечной скорости со скоростью центра масс получаются взаимно перпендикулярные векторы, можно убедиться из рисунка 9. А можно и просто проверить, что скалярное произведение векторов и обращается в ноль в силу того, что модули векторов равны друг другу.

1. Стержень массой m и длиной l шарнирно закреплен за один из концов. Стержень отклонили на некоторый угол от вертикального положения и отпустили. В момент прохождения вертикального положения скорость нижней точки равна υ. Найдите натяжение в средней точке стержня в этот момент времени.

2. Стержень массой m и длиной l вращают в горизонтальной плоскости с угловой скоростью ω вокруг одного из его концов. Найдите зависимость натяжения стержня от расстояния x до оси вращения, если на другом конце закреплен маленький грузик массой М.

3. Найдите период колебаний для системы, описанной в задаче 5 статьи, но для брусков различных масс m₁ и m₂.

4. Выведите известные общие формулы для упругого центрального удара двух шаров, используя переход в систему отсчета центра масс.

5. Шар массой m₁ налетает на покоящийся шар меньшей массы m₂. Найдите максимально возможный угол отклонения налетающего шара при упругом нецентральном ударе.

Читайте также: