12 паркеты из фигур пентамино

Обновлено: 28.04.2024

Полимино (n-мино) — это плоские геометрические фигуры, образованные путем соединения нескольких одноклеточных квадратов по их сторонам. В зависимости от того, из какого количества квадратов полимино состоит, оно может называться по-разному: мономино (n = 1), домино (n = 2), тримино (n = 3), тетрамино (n = 4) и так далее (рис. 1).

Рис. 1. Все возможные (с точностью до вращения и переворачивания) полимино, состоящие не больше чем из четырех квадратов

а) Придумайте три различных замощения плоскости фигурками пентамино, изображёнными слева на рис. 2.

б) Докажите, что существует бесконечно много различных замощений плоскости фигурками нонамино (9-мино), изображенными в центре на рис. 2.

в) Приведите пример фигурки гептамино (7-мино), отличающейся от изображенной справа на рис. 2, копиями которой нельзя замостить плоскость без пробелов и наложений (считаем, что фигурки можно вращать и переворачивать).

Рис. 2. Слева — пентамино, в центре — нонамино, справа — гептамино

Подсказка 1

В пункте а) попробуйте сложить из фигурок пентамино полосу, бесконечную в обе стороны, копиями которой потом можно было бы покрыть плоскость. То же относится к фигуркам нонамино в пункте б).

В пункте в) придумайте такие гептамино, из которых сложить подобную полосу не получится.

Подсказка 2

Чтобы получить много разных замощений, в частности, бесконечно много — как требуется в пункте б), достаточно сконструировать две различные полосы, которые потом можно комбинировать между собой. Три замощения в пункте а) можно получить таким же образом.

А фигура, копиями которой нельзя замостить плоскость, по всей видимости, должна обладать либо выемками, которые нельзя покрыть, либо, наоборот, выступающими частями, которые накладываются друг на друга, как ни крути.

Решение

а) Для начала сложим вместе два наших пентамино — получится восьмиугольник, противоположные стороны которого попарно параллельны (рис. 3).

Такими восьмиугольниками оказывается удобно мостить плоскость. Для этого будем прикладывать их параллельными сторонами друг к другу, образовывая бесконечно длинные полосы. Наиболее естественно это делать одним из двух способов, изображенных на рис. 4.

Полученными полосами покрыть плоскость совсем легко — так у нас получаются два различных замощения данными пентамино, показанные на рис. 5.

Чтобы получить еще одно замощение, посмотрим, как устроены уже построенные нами полосы. Каждая из них представляет собой что-то вроде «лесенки». Считая длину стороны квадрата, из пяти копий которого составлено пентамино, равной единице, мы можем сказать, что у первой «лесенки» длина «ступеньки» равна 3, а высота — 1. Что касается второй «лесенки», то у нее длина и ширина «ступенек» совпадают и равны 2.

Понятно, что если нам удастся сконструировать еще одну полосу-«лесенку», у которой длина и ширина «ступенек» совпадают с одним из уже указанных вариантов, то потом мы сможем скомбинировать между собой эти полосы и получить новое замощение. Удивительным образом эта полоса обнаруживается в одном из двух уже построенных замощений, хотя сама полоса отличается от двух уже известных нам «лесенок» (рис. 6).

Поэтому третье из искомых замощений получается таким, как на рис. 7.

Существуют и более хитрые полосы, которые приводят к замощениям. Один из примеров такого замощения приведен на рис. 8.

б) Самый естественный способ замостить плоскость данными фигурками нонамино заключается в том, чтобы, как и в пункте а), сначала составить из них полоску, а потом уже покрыть все такими полосками (рис. 9, слева).

Другой вариант замощения получается, если мы будем чередовать положения наших фигурок: стандартное, повернутое, стандартное, повернутое и так далее — получается рисунок, похожий на мозаику паззлов (рис. 9, справа).

С первого взгляда кажется совершенно непонятным, что общего между этими двумя замощениями (если не считать форму плитки, которая лежит в их основе, конечно). Дело оказывается в том, что полосы в каждом замощении можно выделять разными способами. В частности, в первом из указанных замощений можно найти полосу, которая имеется и во втором замощении (рис. 10).

Теперь мы можем, чередуя такие полосы с полосами фигурок нонамино, повернутых на 90°, получить бесконечно много разных вариантов замощения плоскости. Например, такой, который изображен на рис. 11.

Проводя аналогию с пунктом а), отметим, что и там мы можем комбинировать две стандартные полосы различными способами, а значит, вариантов замощения плоскости данным пентамино также бесконечно много. А для знакомых с теорией множеств обратим внимание на тот факт, что подобные множества различных замощений даже не являются счетными, поскольку каждому замощению соответствует бесконечная в обе стороны последовательность из нулей и единиц.

в) Среди всех 108 возможных фигурок гептамино только четыре обладают тем свойством, что их копиями нельзя замостить плоскость без пробелов и наложений: одна из них изображена справа на рис. 2, а остальные три — на рис. 12. Мы приведём доказательство этого факта только для левой из этих трех фигурок. Для двух других объяснение использует ту же самую идею, хотя и является более громоздким из-за необходимости рассмотрения большего числа случаев.

Рассмотрим данную фигурку гептамино и одну из клеток, которая к ней примыкает по двум сторонам (зелёная клетка на рис. 13). Эта клетка должна быть покрыта какой-либо копией фигурки гептамино — с точностью до симметрии имеется всего два варианта такого покрытия. Для каждого из этих вариантов рассмотрим одну из клеток, которая примыкает по двум сторонам ко второй фигурке (жёлтые клетки на рис. 13). Она тоже должна быть покрыта некоторой копией данной фигурки гептамино. Однако как бы мы ни располагали третью фигурку, а впоследствии и остальные фигурки, соседняя клетка (красные клетки на рис. 13) окажется не покрыта ничем. Следовательно, данная фигурка гептамино не допускает замощения плоскости без пробелов и наложений.

Послесловие

Термин полимино (англ.: polyomino) был введен в широкое обращение американским математиком Соломоном Голомбом в 1953 году, а затем популяризирован Мартином Гарднером. Однако это вовсе не означает, что до середины XX века человечество было совершенно незнакомо с этим понятием. Как справедливо отмечал сам Голомб, задачи о пентамино упоминаются еще в книге «Кентерберийские головоломки» английского изобретателя головоломок и развлечений Генри Дьюдени (Henry Dudeney), изданной в 1907 году, и есть основания полагать, что Дьюдени был не первым человеком, заинтересовавшимся этой темой. Кроме того, в период с 1937-го по 1957 годы в английском журнале Fairy Chess Review появился ряд статей, в которых рассматривались задачи разбиения различных фигур на части, имеющие форму n-мино для n = 1, . 6.

Различают три вида полимино в зависимости от того, разрешается ли переворачивать и вращать фигурки. Двусторонние полимино (англ.: free polyominoes) можно как переворачивать, так и поворачивать, односторонние полимино (англ.: one-sided polyominoes) можно только поворачивать в плоскости, а фиксированные полимино (англ.: fixed polyominoes) нельзя ни поворачивать, ни переворачивать. Существует ровно по одному типу двусторонних мономино и домино, два типа тримино и пять типов тетрамино (рис. 1). Количество различных фигурок двустороннего пентамино равно уже двенадцати (рис. 14). Чтобы запомнить их все, Голомб предложил использовать следующее мнемонеческое правило: каждой фигурке пентамино сопоставим букву латинского алфавита; семь из этих букв (TUVWXYZ) составляют конец латинского алфавита, а еще пять (FILPN) входят в имя Filipino (в оригинале книги Голомба слово «Filipino» означает «филиппинец»). К слову, тетрамино тоже иногда обозначают латинскими буквами: I, O, T, L и Z.

Чем больше число n, тем большее количество различных n-мино можно составить из n единичных квадратиков, причем зависимость является экспоненциальной. Так, существует 35 различных разновидностей двустороннего гексамино, 108 разновидностей двустороннего гептамино, 369 разновидностей двустороннего октамино и более тысячи видов фигурок двустороннего нонамино. Точную формулу, которая бы отражала зависимость количества различных фигурок n-мино от числа n, пока еще никому не удалось найти, а потому в каждом конкретном случае приходится пускаться в утомительные вычисления, отнимающие уйму времени. На сегодняшний день с использованием суперкомпьютеров удалось перечислить всевозможные двусторонние полимино для всех n ≤ 28, а также всевозможные фиксированные полимино для всех n ≤ 56 — количество разновидностей последних составляет приблизительно 7·10 31 штук.

Большая часть популярных задач и головоломок, использующих фигурки полимино, связана с замощениями плоскости или различных других объектов — квадратов, прямоугольников и фигур более хитрой формы. Не претендуя на то, чтобы охватить все, что познало человечество за последние пятьдесят с лишним лет, перечислим наиболее заметные и любопытные идеи и факты.

1. Задача, уже ставшая классической: можно ли покрыть фигурками домино 1×2 шахматную доску 8×8, из которой вырезана пара противоположных угловых клеток? Ответ на поставленный вопрос отрицательный: раскрасив доску так, как это показано на рис. 15, легко убедиться, что эта доска содержит 32 черные и 30 белых клеток, в то время как каждая фигура домино занимает по одной клетке каждого цвета, как бы мы ее ни располагали.

2. Другая задача, похожая на первую: какую клетку из шахматной доски 8×8 нужно вырезать, чтобы ее можно было покрыть фигурками тримино 1×3? Чтобы решить ее, оказывается полезным раскрасить доску в три цвета так, как изображено слева на рис. 16. При такой раскраске черных и белых клеток поровну — по 21 штуке, а серых клеток больше — их 22. Поскольку каждая фигурка тримино занимает по одной клеточке каждого цвета, мы должны вырезать серую клетку. Однако подойдет не любая серая клетка, а лишь такие, которые при повороте доски перейдут в серые клетки — таких всего четыре (рис. 16, в середине). Одно из возможных покрытий показано справа на рис. 16.

3. Шахматную доску можно покрыть копиями каждого вида тетрамино, кроме Z-тетрамино. При этом нельзя покрыть ее одним квадратом и 15-ю T-тетрамино, одним квадратом и 15-ю L-тетрамино, а также одним квадратом и 15-ю I-тетрамино (для доказательства этих фактов также используются различные раскраски доски 8×8).

4. Шахматную доску можно покрыть полным набором двусторонних пентамино и квадратным тетрамино, использовав каждую фигурку ровно один раз. При этом квадрат может быть расположен в любой части доски. Обобщение этой головоломки — покрыть полным набором двусторонних пентамино шахматную доску с произвольными четырьмя вырезанными клетками. Большинство таких задач имеют решение. Несколько примеров приведено на рис. 17.

5. Полным набором двусторонних пентамино можно покрыть прямоугольники размера 6×10, 5×12, 4×15 и 3×20. При этом количество возможных решений (с точностью до поворота и отражения данного прямоугольника) для случая 6×10 составляет 2339 различных укладок, для случая 5×12 — 1010 укладок, для случая 4×15 — 368 укладок, а для случая 3×20 — всего 2 укладки. Примеры показаны на рис. 18

6. Задача об утроении заключается в следующем: выбрав одну из 12 фигур пентамино, необходимо построить из каких-либо 9 оставшихся пентамино фигуру, подобную выбранной, но в 3 раза большей длины и ширины. Решение существует для любого из 12 пентамино, причем оно далеко не единственно (количество решений варьируется от 15 для Х-пентамино до 497 для Р-пентамино). На рис. 19 показано решение, найденное А. ван де Ветерингом. Оно обладает интересным свойством: каждое пентамино используется для утроения девяти из остальных, по одному разу в каждой. То есть из девяти комплектов пентамино можно одновременно сложить все 12 утроенных пентамино.

7. Полным набором двусторонних гексамино никакой прямоугольник покрыть нельзя. Для доказательства достаточно использовать обычную шахматную раскраску. В любом прямоугольнике при такой раскраске количество черных и белых клеток будет совпадать. А вот в наборе гексамино эти числа обязательно будут различаться, потому что 24 фигурки гексамино занимают по 3 белые и черные клетки, а оставшиеся 11 фигурок — 2 клетки одного цвета и 4 клетки другого цвета.

8. Зато полным набором двусторонних гексамино можно покрыть разные другие интересные симметричные фигуры (рис. 20).

9. Особое место среди задач этой тематики занимают покрытия разных объектов фигурками домино. Так, количество покрытий прямоугольника 2×n фигурками домино выражается (n + 1)-м числом Фибоначчи. Существует также формула для числа покрытий фигурками домино прямоугольника 2m×2n, она имеет следующий вид:

10. Любая из фигурок мономино, домино, тримино, тетрамино и пентамино допускает моноэдральное замощение плоскости. Это означает, что какую из перечисленных фигурок мы ни возьмем, плоскость можно покрыть ее копиями без пробелов и наложений. При этом для всех фигурок, за исключением X-пентамино, таких замощений бесконечно много.

11. Любая из 35 фигурок гексамино допускает моноэдральное замощение плоскости. Среди 108 фигурок гептамино четыре таким свойством не обладают. Это же можно сказать про 26 из 369 фигурок октамино и 235 из 1285 фигурок нонамино.

12. Существуют наборы из нескольких фигурок полимино, которые допускают только непериодические замощения. Например, таковыми являются наборы фигурок полимино, изображённые на рис. 21.

Рис. 21. Наборы полимино, допускающие только непериодические заполнения плоскости

Помимо полимино существуют и другие объекты, имеющие сходные строение и свойства. Речь идет, прежде всего, о полиамондах, полигексах и полиаболах, то есть о фигурах, составленных из нескольких правильных треугольников, правильных шестиугольников и равнобедренных прямоугольных треугольников соответственно. Кроме того, интерес представляют пространственные полимино, которые называются поликубами.

При подготовке задачи были использованы следующие материалы:
1) М. Гарднер, «Математические головоломки и развлечения», М: Мир, 1971.
2) М. Гарднер, «Математические новеллы», М: Мир, 1974.
3) С. В. Голомб, «Полимино», М: Мир, 1975.
4) Г. Дьюдени, «Кентерберийские головоломки», М: Мир, 1979.
5) B. Grünbaum, G. C. Shephard, Tilings and Patterns, 1987.

Полимино — фигуры, образованные путём соединения нескольких клеток по их сторонам. Например, тетрамино — полимино из четырёх клеток, всего таких 5 штук (рис. 1). А полимино из пяти клеток называется пентамино, есть 12 различных фигур (рис. 2).

На Математическом празднике 2018 года в 7 классе была моя задача:

Существует ли такая фигура, что при любом выборе вида тетрамино эту фигуру можно составить, используя тетраминошки только выбранного вида? (Переворачивать тетраминошки можно.)

Ответ тут положительный (рис. 3).

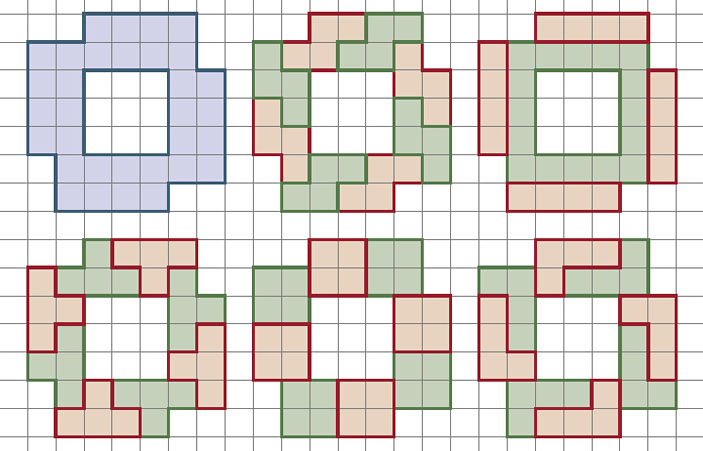
Зададим тот же вопрос про пентамино. Оказывается, здесь ситуация другая: нет такой фигуры, что при любом выборе вида пентамино эту фигуру можно составить, используя пентаминошки только выбранного вида. Почему?

Докажем, что нет даже такой конечной фигуры, которая «делится» только на кресты (рис. 4) и только на арки (рис. 5). Пусть какую-то фигуру можно разделить на кресты. Рассмотрим множество самых правых её клеток, из них возьмём самую верхнюю (клетка 1 рисунка 6). В силу выбора клетки 1, фигуре не принадлежат клетки выше клетки 1 в том же столбце и все клетки правее клетки 1 (серая зона на рисунке 6). Тогда крест, накрывающий клетку 1, может стоять только как на рисунке 6. А клетки 2 и 3 не могут принадлежать фигуре, так как любой крест, содержащий одну из этих клеток и не пересекающийся с первым крестом, захватит клетку из серой зоны. Но тогда внутри фигуры не удастся расположить арку, покрывающую клетку 1.

Интересно, для какого наибольшего числа видов пентамино всё же существует фигура, «делящаяся» на каждый из них? На рисунке 7 приведён пример фигуры для 4 видов.

Точный ответ на этот вопрос нам неизвестен. Попробуйте поэкспериментировать и найти фигуру, «делящуюся» на как можно большее число видов пентамино. В следующем номере мы приведём лучший известный нам результат. Если у вас получится пример, в котором больше видов, обязательно пришлите его нам для публикации. Удачи!

Нам известен пример Джорджа Сичермана. Придуманную им фигуру можно разделить на 8 видов пентамино (см. рисунок).

В настоящее время в методике обучения математике большое внимание уделяется проблеме построения пропедевтических курсов геометрии. Основной методической линией этих курсов является организация специальной геометрической деятельности учащихся.

Мы создали и апробировали программу по изучению геометрического материала для 5–6-х классов (она была частично опубликована в газете «Математика» за 2000 г., № 18), реализация которой также предполагает включение учащихся в геометрическую деятельность. Для усвоения в полном объеме всеми аспектами содержания предложенного нами пропедевтического курса геометрии, учащиеся, на доступном им уровне, должны овладеть компонентами геометрической деятельности: логическим, пространственным, интуитивным, метрическим, конструктивным, символическим. В содержание курса включена система предметно-практических, прикладных задач и упражнений, а также разнообразные развивающие игры: оригами, танграм, стомахион и другие.

Элементы игры вырезаны из квадратного (3×3) куска паркета, состоящего из рядов квадратных плиток, сдвинутых на половину стороны. Всего получится 10 комбинаций — элементов, составленных из четырех квадратов (рис.1). Используя этот набор, сложите геометрические фигуры, изображенные на рис.2. Для фигуры № 5 дано решение. Придумайте также другие фигуры, которые можно сложить из элементов тетрамино—паркета.

Имеются шесть бумажных прямоугольных полосок с соотношением сторон 4×1 и фломастер. Раскрасьте полоски, как показано на рис. 3. Накладывая полоски друг на друга (переплетения запрещены), составьте заданный узор. Последовательность составления узора показана на рис. 4. Составьте, описанным выше способом, узоры представленные на рис. 5.

Новые материалы:

Военно-спортивная полоса препятствий для 10-11-х классов :: Урок изучения новой темы по ОБЖ во 2-м классе по теме «Меры безопасности при общении с домашними животными» :: Внеклассное мероприятие для учащихся 6–7-х классов на тему: «По тропинкам мифологического Египта» :: Разработка внеклассного мероприятия «Моя малая родина» :: Конспект урока по ОБЖв 11-м классе по теме «Основные понятия о воинской обязанности» :: Конверт, 2017 :: Дом и дача/Мебель/Мебель/Прихожие/Обувницы/Тумбы / Вентал / Тумба для обуви Viva-3 10000164 ::

• 0.1 Отзывы (через аккаунты в социальных сетях Вконтакте, Facebook или Google+):
  • 0.1.1 Оставить отзыв с помощью аккаунта ВКонтакте:
  • 0.1.2 Оставить отзыв с помощью аккаунта FaceBook:
  • 1.1 Полимино
  • 1.2 Домино
  • 1.3 Тримино
  • 1.4 Тетрамино
  • 1.5 Пентамино

  Отзывы (через аккаунты в социальных сетях Вконтакте, Facebook или Google+):
  

  Оставить отзыв с помощью аккаунта ВКонтакте:
  

  Оставить отзыв с помощью аккаунта FaceBook:
  

  Разделы: Математика, Конкурс «Презентация к уроку»

  Презентация к уроку
  

  Загрузить презентацию (2 МБ)

  Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

  Полимино
  

  В этой статье мы будем рассматривать полимино — фигуры, составленные из одноклеточных квадратов так, что каждый квадрат примыкает хотя бы к одному соседнему, имеющему с ним общую сторону.

  Задачи с полимино очень характерны для комбинаторной геометрии — раздела математики, занимающегося вопросами взаимного расположения и комбинирования геометрических фигур. Это очень красивая, но еще почти не разработанная ветвь математики, поскольку общих методов в ней, по-видимому, очень мало, а известные ныне методы настолько примитивны, что не поддаются усовершенствованию. Многие встречающиеся в практике важные инженерные задачи — в первую очередь те, которые связаны в том или ином смысле с оптимальным расположением фигур заданной формы, — по существу относятся к комбинаторной геометрии.

  В последующих комбинаторных задачах предполагается, что полимино можно вращать (то есть поворачивать на 90, 180 или 270) и зеркально отражать (переворачивать), не меняя формы самих фигур.

  Домино
  

  Домино состоит из двух квадратов и может иметь лишь одну форму — форму прямоугольника размером 1×2 (см. рис. 1). Первая связанная с домино задача, вероятно, многим знакома: даны шахматная доска, из которой вырезана пара противоположных угловых клеток, и коробка домино, каждое из которых покрывает ровно две клетки шахматной доски (см. рис. 2). Возможно ли целиком покрыть доску с помощью 31 кости домино (без свободных клеток и наложений)? Ответ на этот вопрос гласит: «НЕТ» и имеет замечательное доказательство. Шахматная доска содержит 64 чередующиеся клетки белой и черной раскраски (имеется в виду обычная шахматная раскраска доски). Каждая положенная на такую доску и покрывающая две соседние клетки кость домино покроет одно белое и одно черное поле, а n костей домино — n белых и n черных полей, т.е. поровну и тех и других. Но изображенная на рисунке шахматная доска содержит больше черных клеток, чем белых, и потому ее нельзя покрыть костями домино. Этот результат есть типичная теорема комбинаторной геометрии.

  
  

  Тримино
  

  Тримино (или триомино) — полимино третьего порядка, то есть многоугольник, полученный путём объединения трёх равных квадратов, соединённых сторонами. Если повороты и зеркальные отражения не считать различными формами, то существует только две «свободных» формы тримино (см. рис.3): прямое (I-образное) и угловое (L-образное).

  Тетрамино
  

  С тетрамино связано множество задач на составление из них разных фигур. Доказано, что сложить какой-либо прямоугольник из полного набора тетрамино невозможно. Доказательство использует раскраску в шахматном порядке. Все тетрамино, кроме Т-образного, содержат 2 чёрные и 2 белые клетки, а Т-образное тетрамино — 3 клетки одного цвета и 1 клетку другого. Поэтому любая фигура из полного набора тетрамино (см. рис.4) будет содержать клеток одного цвета на две больше, чем другого. Но любой прямоугольник, с чётным количеством клеток, содержит равное число чёрных и белых клеток.

  Пентамино
  

  
  

  Полимино, покрывающее пять клеток шахматной доски, называются пентамино. Существует 12 видов пентамино, которые можно обозначить прописными латинскими буквами, как указано на рисунке (см. рис. 5). В качестве приема, позволяющего легко запомнить эти наименования, укажем, что соответствующие буквы составляют конец латинского алфавита (TUVWXYZ) и входят в имя FiLiPiNo. Поскольку всего имеется 12 разных пентамино и каждая из этих фигур покрывает пять клеток, то вместе они покрывают 60 клеток.

  Самая распространённая задача о пентамино — сложить из всех фигурок, без перекрытий и зазоров, прямоугольник. Поскольку каждая из 12 фигур включает в себя 5 квадратов, то прямоугольник должен быть площадью 60 единичных квадратов. Возможны прямоугольники 6×10, 5×12, 4×15 и 3×20 (см. рис. 6).

  Для случая 6×10 эту задачу впервые решил в 1965 году Джон Флетчер. Существует ровно 2339 различных укладок пентамино в прямоугольник 6×10, не считая поворотов и отражений целого прямоугольника, но считая повороты и отражения его частей (иногда внутри прямоугольника образуется симметричная комбинация фигур, поворачивая которую можно получить дополнительные решения).

  Для прямоугольника 5×12 существует 1010 решений, 4×15 — 368 решений, 3×20 — всего 2 решения (отличающихся вышеописанным поворотом). В частности, существует 16 способов сложить два прямоугольника 5×6, из которых можно составить как прямоугольник 6×10, так и 5×12.

  Еще одна интересная задача о пентамино — задача об утроении фигур пентамино (см. рис. 7). Эта задача была предложена профессором Калифорнийского университета Р.М.Робинсоном. Выбрав одну из 12 фигур пентамино, необходимо построить из каких-либо 9 из 11 оставшихся пентамино фигуру, подобную выбранной, но в 3 раза бо́льшей длины и ширины. Решение существует для любого из 12 пентамино, причём не единственное (от 15 решений для Х до 497 для Р). Существует вариант этой задачи, в котором для построения утроенной фигуры разрешается использовать также и саму исходную фигуру. В этом случае число решений от 20 для Х до 9144 для Р-пентамино.

  
  

  Игры с пентамино (часть 4). Курс наглядной геометрии 5-6 класс. Паркеты из фигур пентамино.

  Просмотр содержимого документа
  «Игры с пентамино (часть 4). Курс наглядной геометрии 5-6 класс.»

  
  

  Цикл уроков наглядной геометрии: «Геометрия на клетчатой бумаге»

  
  

  Игры с пентамино (часть 4)

  
  

  Паркеты из фигур пентамино

  
  

  Формулируем определение

  Используя различные источники информации (учебники, интернет и т.д.) сформулируйте определение:

  Паркет – это…

  
  

  Формулируем определение

  Паркет – это вид напольного деревянного покрытия , представляющий из себя разбиение плоскости многоугольниками , без пробелов и перекрытий.

  
  

  Формулируем определение

  Паркет – вид деревянного напольного покрытия, представляющий из себя разбиение плоскости на многоугольники , между которыми нет пробелов и перекрытий, и образующий узор из повторяющихся фрагментов ….

  
  

  Игры с пентамино (часть 4). Курс наглядной геометрии 5-6 класс. Паркеты из фигур пентамино.

  Просмотр содержимого документа
  «Игры с пентамино (часть 4). Курс наглядной геометрии 5-6 класс.»

  
  

  Цикл уроков наглядной геометрии: «Геометрия на клетчатой бумаге»

  
  

  Игры с пентамино (часть 4)

  
  

  Паркеты из фигур пентамино

  
  

  Формулируем определение

  Используя различные источники информации (учебники, интернет и т.д.) сформулируйте определение:

  Паркет – это…

  
  

  Формулируем определение

  Паркет – это вид напольного деревянного покрытия , представляющий из себя разбиение плоскости многоугольниками , без пробелов и перекрытий.

  
  

  Формулируем определение

  Паркет – вид деревянного напольного покрытия, представляющий из себя разбиение плоскости на многоугольники , между которыми нет пробелов и перекрытий, и образующий узор из повторяющихся фрагментов ….

  Читайте также:

    
  • Сравнение фасадных панелей под кирпич
    
  • Восстановление бетонных стен каналов после ремонтных работ
    
  • Гидроизоляция под кирпичную кладку
    
  • Клумба из кирпича своими руками
    
  • Расчет крена плитного фундамента